【試験対策】線形代数の前期授業の要点が30分で分かるよう凝縮しました

2019年7月19日作成2022年5月21日更新

こんにちは、おぐえもん(@oguemon_com)です。

そろそろ期末試験のシーズンですね！このサイトに来る人の多くは試験勉強目的です。そこで、勉強を手取り早くできるように前期の線形代数講義で扱った内容をざっくりと振り返りましょう。

行列の定義と演算

行列とは

まず、線形代数では行列とベクトルを主に扱います。

行列とは、数字を格子状に並べたひとまとまりのことです。並べる個数は以下の例に限らず様々です(例えば $5 \times 3$ など)。行列を構成する各々の数字のことを成分と呼びます。

行列

A= \left[ \begin{array}{ccc} 1 & 2 & 1 \\ 3 & 4 & 2 \\ 2 & 3 & 3 \end{array} \right]

行列には、足し算や掛け算などの演算ルールが、今まで扱ってきた数とは別に用意されています。今まで扱ってきた数(3 とか-1.5 とか)のことをスカラーと呼び、行列と区別します。

行列の横向きのひと並びを行、縦向きのひと並びを列といいます(行と列の混合に注意！)。行が 1 つしかない(つまり横 1 列の)行列を行ベクトル、列が 1 つしかない(つまり縦 1 列)の行列をベクトルといいます。行ベクトルと列ベクトルを総称してベクトルといいます。

ベクトル

\boldsymbol{a}= \left[ \begin{array}{ccc} 1 & 4 & 3 \end{array} \right]

線形代数では、行列はアルファベットの大文字で、ベクトルはアルファベットの太字で表記するのがメジャーです。

その他の細かいことは次のページに記しています。

行列の定義・用語

おぐえもん.com

足し算・スカラー倍・掛け算

行列同士の足し算(引き算)は、それぞれ対応する成分を足す(引く)だけです。サイズの異なる行列同士は足し引きできません。

行列の足し算

\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right]+ \left[ \begin{array}{cc} 3 & -1 \\ -2 & 1 \end{array} \right]= \left[ \begin{array}{cc} 4 & 1 \\ 1 & 5 \end{array} \right]

行列は、スカラーを掛け合わせることができます(スカラー倍)。この時、全ての成分にスカラーを掛けます。スカラー倍はどんなサイズの行列でもできます。

行列のスカラー倍

4\left[ \begin{array}{cc} 1 & -2 \\ -3 & 4 \end{array} \right]= \left[ \begin{array}{cc} 4 & -8 \\ -12 & 16 \end{array} \right]

行列の掛け算が難所です。次のように複雑な計算方法を持ちます。左の行列の横の個数と、右の行列の縦の個数が同じでないと掛け算できません。

行列の掛け算

\left[ \begin{array}{cc} a & b \\ c & d \end{array} \right] \left[ \begin{array}{cc} w & y \\ x & z \end{array} \right]= \left[ \begin{array}{cc} aw+bx & ay+bz \\ cw+dx & cy+dz \end{array} \right]

行列の掛け算の丁寧な解説など、演算に関することは次のページをご覧ください。

行列の演算

おぐえもん.com

零行列と単位行列

行列の中でも名前がついた特別なものがあります。

零行列は、全ての成分が 0 の行列です。 $O$ と表します。

零行列

O=\left[ \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right]

零行列は、足し算や掛け算において、まるでスカラーの 0(ゼロ)のように振る舞います。

A+O=A, \ O+A=A

AO=O, \ OA=O

単位行列は、対角成分が 1 で、それ以外の成分が 0 の行列です。 $E$ や $I$ と表します。単位行列は正方行列(列と行の数が同じ行列)であることが前提です。

単位行列

E=\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]

単位行列は、ある行列に掛け合わせても、その行列の値を変えません。掛け算においてまるでスカラーの 1 のように振る舞います。

AE=A

EA=A

正則行列と逆行列

これは、正方行列のみの話です。ある行列 $A$ について、掛け合わせると積が単位行列 $E$ になる行列が存在する場合があります。このような行列を逆行列と呼び、 $A^{-1}$ と書きます。また、逆行列を持つ行列を正則行列といいます(正方行列と字面が紛らわしいので注意！)。

AA^{-1}=E

逆行列はスカラーでいう逆数(ある数に対して掛けると 1 になる数)みたいな存在です。まるで-1 乗しているような見た目をしていますが、行列には割り算の概念がないので、決して-1 乗しているわけでありません。あくまで便宜上の表記です。

逆行列の例や簡単な性質はこちらで紹介しています。

正則行列と逆行列

おぐえもん.com

注意すべき性質

行列の性質の多くはスカラーの性質と共通しますが、スカラーと大きく異なる性質に注意する必要があります。

まず、行列の積には交換法則がありません。つまり、掛け算の順序を入れ替えると結果が異なることがあります(というかほとんどの場合異なります)。行列の積を考える際は順序にも気を使わなければなりません。

そして、行列には零因子というものがあります。

零因子

$A \neq O$ かつ $B \neq O$ であるにも関わらず、

AB=O

となる行列 $A,B$ が存在し、この行列を零因子という。

スカラーだと、 $ab=0$ なら、 $a$ か $b$ のどちらか最低 1 つが 0 ですが、行列は決してそんなことはありません。

その他、行列には様々な性質があります。それらを次のページにまとめています。

注意すべき行列の性質

おぐえもん.com

連立方程式×行列

連立方程式と行列

行列と連立方程式は密接な関係にあります。というのも、行列は、連立方程式を簡潔に記述できる存在だからです。例えば、次のような連立方程式を用意します。

\left\{ \begin{array}{rclc} 5x-2y&=&5 &(1) \\ x+y&=&8 &(2) \end{array} \right.

これを行列とベクトルを用いて簡単に表せます。実際に積のルールに従って計算して結果を確かめましょう。

\left[ \begin{array}{cc} 5 & -2 \\ 1 & 1 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 5 \\ 8 \end{array} \right]

連立方程式の解の性質は、係数の組み合わせや右辺の値がキモになります。そこで、これらを行列(ベクトル)の形にまとめることで性質に関する議論を簡単に行えるようにするのです。

連立方程式の解き方

線形代数に取り組む賢いみなさんは連立方程式を解くことくらいお茶の子さいさいでしょう。ここでは、連立方程式の解き方を詳しく説明しません。ただし、解く上で各式に対して次に掲げる変形をしていることを思い出してください。

ある方程式を何倍かにする
ある方程式を何倍かにしたものを他の方程式に加える
ある2つの方程式を入れ替える

ちなみに、このような解き方を消去法といいます。

階段行列と階数(rank)

連立方程式を行列で扱う今、連立方程式の解き方を行列を用いて説明することができます。ここで、連立方程式の係数をまとめた行列を係数行列、係数行列の右に右辺のベクトルを繋げた行列を拡大係数行列といいます。

先ほどの連立方程式の例だと、拡大係数行列は次の通り。

\left[ \begin{array}{ccc} 5 & -2 & 5\\ 1 & 1 & 8 \end{array} \right]

これに、消去法を用いるとき、先ほど連立方程式の各式に行ってきた変形操作は、係数拡大行列の各行に対する次の操作に置き換えられます。

ある行を何倍かにする
ある行を何倍かにしたものを他の行に加える
ある2つの行を入れ替える

これを行基本操作といいます。

さて、行基本操作を繰り返すと、やがて次の形の行列が現れます。

\left[ \begin{array}{ccc} 1 & 1 & 8\\ 0 & 1 & 5 \end{array} \right]

このような、行を下るほど左から連なるゼロの数が増える行列を階段行列といい、階段行列で 0 でない成分が存在する行の数を階数(rankA)といいます。

ある行列の階数は、途中の行基本操作の手順に関わらず同じです。階数は、連立方程式が解をもつのか否かを判断する重要な材料になります。

【連立方程式編】消去法と階段行列

おぐえもん.com

正則行列と連立方程式

連立方程式の係数行列 $A$ が正方行列であるときを考えましょう。ちなみにどの連立方程式についても適宜 0 成分で埋めると正方行列に仕立て上げられます。

$A$ が逆行列を持つか否かは、連立方程式の解や行列の階数、行基本操作などの観点から立てた様々な命題にリンクします。

$n$ 次の正方行列 𝐴 について、以下の 4 つの命題は同値である。

$A$ は正則行列である。
連立一次方程式 $A\boldsymbol{x}=\boldsymbol{b}$ が有する解は1組のみである。
$A$ の階数について、 ${\rm rank}A=n$ が成り立つ。
$A$ は、行基本操作によって単位行列 $E$ に変換することができる。

少なくとも 1.と 2.の同値関係はおさえてくださいね。

これらの関係性の詳細については、次のページで解説しています。

【連立方程式編】連立方程式と正則行列の関係

おぐえもん.com

行列式

行列式とは

行列式は、行列の特徴を表す指標の 1 つです。全ての正方行列が、それぞれ 1 つずつ行列式を持ちます。行列式なんて言いますが、方程式ではなく、スカラーの値を取ります。

行列 $A$ の行列式は、 $|A|$ や ${\rm det}(A)$ と表します。「det」は、行列式の英語に当たる”determinant”に由来します。

行列式が最も活躍するのは、逆行列を導出する場面です。逆行列は、連立方程式の答えを瞬時に導く重要な存在です。ある行列がそもそも逆行列を持つのかを行列の値から判断できます（先に言うと、 $|A|=0$ なら逆行列なし、そうでないなら逆行列ありです）。また、逆行列の導出にも行列式が用いられます。

2x2と3x3行列での定義

線形代数の授業で頻出する 2 次正方行列と 3 次正方行列における行列式の求め方を学習しましょう。ちなみに、行列式は正方行列でない行列(長方形の行列やベクトル)にはありません。

2 次正方行列での定義は、次の通り。

A=\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]

について、

|A|=a_{11}a_{22}-a_{12}a_{21}

要は、「（左上 × 右下）-（右上 × 左下）」です。

3 次正方行列での定義は、次の通り。一気に複雑化します。

A=\left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right]

について、

\begin{array}{rr} |A|=&a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\ &-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32} \end{array}

次の画像だと分かりやすいかもしれません。

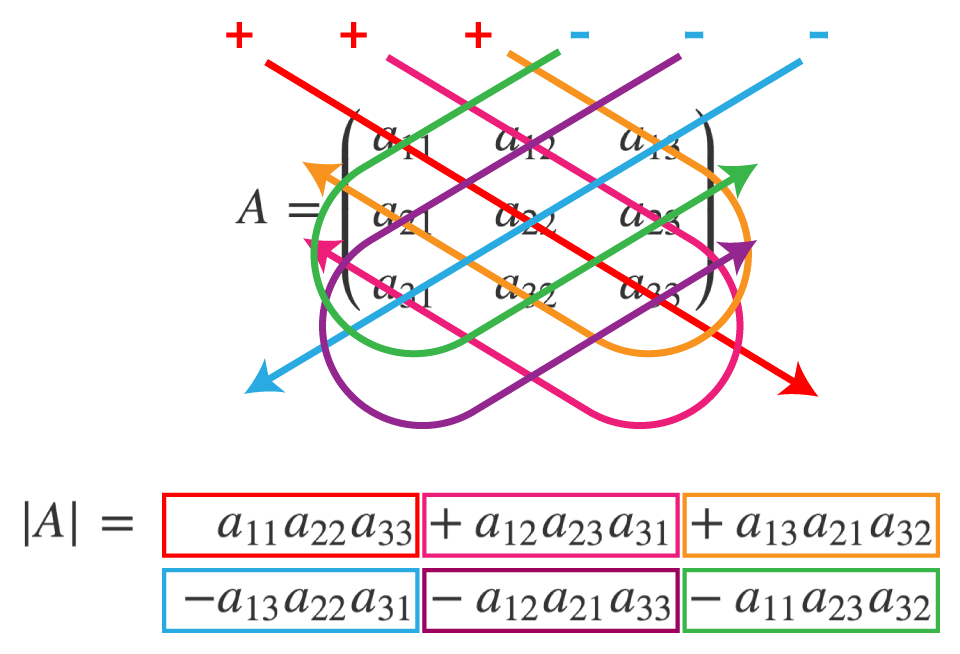
具体的な計算例は次のページに詳しく載せています。

行列式って何？

おぐえもん.com

4 次以上の正方行列の行列式については次のページをご覧ください。

【行列式編】行列式の定義

おぐえもん.com

行列式の性質

ここでは行列式が持つ主な性質をご紹介します。

まず、行列 $A$ の行と列を入れ替えた、いわゆる転置の行列 $^tA$ の行列式は、元の行列式と同じです。これから行列の行基本操作に絡めて行列式の性質を見るのですが、そこで述べられる性質は、行を列に置き換えて考えても同じということです。

|A|=|^tA|

「行基本操作 1：ある行を何倍かにする」について、行列 $A$ のある行を $\lambda$ 倍すると、その行列式は元の $\lambda$ 倍である $\lambda|A|$ になります。この性質から、ある行が全部 0 の行列の行列式は必ず 0 になります。これは、その行を 0 倍したときの場合の結果に相当するからです。

「行基本操作 2：ある行を何倍かにしたものを他の行に加える」について、ある行に他の行のスカラー倍を加えても、行列式は一切変化しません。つまり、行基本操作 2 をする前後の行列は行列式が全く同じということです。

「行基本操作 3：ある 2 つの行を入れ替える」について、2 つの行を入れ替えたら、行列式の符号（+-）が反転します。

以上の性質を駆使すると、行基本操作を経てたどり着いた簡単な行列の行列式をサクッと求めたら、行基本操作をさかのぼりつつ適宜行列式をスカラー倍したり符号を入れ替えたりするだけで元の行列式を求めることができます。

以上の性質の詳しい説明や、その他の重要な性質は次のページをご覧ください。

【行列式編】行列式の性質

おぐえもん.com

逆行列

逆行列の求め方

逆行列の求め方は、大きく分けて二種類あります。

1 つ目は、行基本操作を駆使する方法です。

ある $n$ 次の正則行列 $A$ と、同じく $n$ 次の単位行列 $E$ を左右に繋げた、 $n \times 2n$ の行列 $[A \ E]$ を用意する。

行列 $[A \ E]$ に対して行基本操作を駆使して、左側が単位行列の形、つまり $[E \ P]$ の形に変形したとき、 $P$ は $A$ の逆行列である。

なぜ成り立つか、具体的な計算例は次のページで紹介しています。

【連立方程式編】連立方程式と正則行列の関係

おぐえもん.com

2 つ目は、余因子というものを活用する方法です。以下の公式を見れば分かるように、行列式 $|A|$ が 0 ならば逆行列は定義できない、つまり逆行列が存在しません(0 でないなら存在します)。余因子については後で説明します。

$A_{ij}$ は、正方行列 $A$ の $i$ 行 $j$ 列成分の余因子とする。

正方行列 $A$ が逆行列を持つとき、逆行列 $A^{-1}$ は次式で表せる。

\begin{aligned} A^{-1} &=\frac{1}{|A|}{}^t[A_{ij}] \\ &=\frac{1}{|A|} \left[ \begin{array}{cccc} A_{11} & A_{21} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{array} \right] \end{aligned}

成り立つ理由をはじめとする詳細は次のページをご覧ください。

【行列式編】逆行列の求め方を画像付きで解説！

おぐえもん.com

余因子と余因子展開

余因子とは、ある行と列をカットして残った一回り小さい行列の行列式に、正負の符号を加えたスカラー値です。符号は、列番号と行番号の和の偶奇で正負が決まります。正方行列 $A$ の $i$ 行目と $j$ 列目をカットして作る余因子を $A_{ij}$ と記します。これを直感的に表現したのが次の画像です。

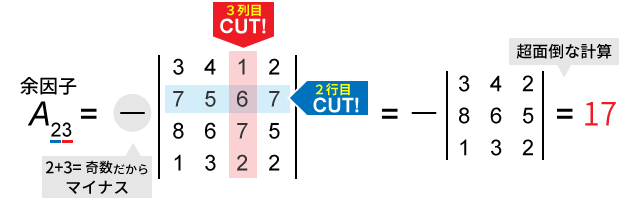
余因子展開とは、ある行列の行列式を、余因子を用いた多項式の形に展開することをいいます。というのも、同じ行（または列）を構成する全ての成分について「成分の値 × 成分の余因子」を全て足し合わせた値は、行列式と等しくなるのです。

余因子展開

行列 $A$ に対する $(i,j)$ 成分の余因子を $A_{ij}$ とする。

この時、行列 $A$ のそれぞれの行について次の式が成り立つ。

|A|=a_{i1}A_{i1}+a_{i2}A_{i2}+\cdots+a_{in}A_{in}

それぞれの列についても同様である。

余因子展開を使って行列式を計算することはほとんどありません。しかし、余因子展開を用いることで、余因子を用いた逆行列の公式が成立する理由を説明できるようになります。ですので線形代数の講義では必ずと言えるほど登場します。

余因子と余因子展開について詳しくはこちらで説明しています。

余因子と余因子展開

おぐえもん.com

連立方程式x行列(part2)

クラメルの公式

これは、連立方程式の解を、行列式を用いたスッキリとした式で表すことができる定理です。

連立方程式 $A\boldsymbol{x}=\boldsymbol{b}$ について、その解 $\boldsymbol{x}$ の第 $i$ 成分を $x_i$ とする。

このとき、以下の式が成立する。

x_i=\frac{|A_i|}{|A|}

ここで、 $A_i$ は、行列 $A$ の $i$ 列目を、連立方程式の右辺 $\boldsymbol{b}$ に置き換えた行列である。

この公式、見た目こそシンプルですが、実際に活用するとなると、(解の成分数+1)個の行列式を求めなければならないので計算がしんどいです。ですので、実用性には欠けます。

具体的な計算例を次のページに掲載しています。

【行列式編】「クラメルの公式」で連立方程式を行列式で表す！

おぐえもん.com

連立方程式の解と行列式

行列式の値を見ると、連立方程式の解の組数を知ることができます。

まずは、連立方程式 $A\boldsymbol{x}=\boldsymbol{b}$ について。このとき、行列式 $|A|$ が 0 でないなら、解は 1 組のみになります。 $|A| \neq 0$ なら逆行列 $A^{-1}$ が存在し、解が $\boldsymbol{x}=A^{-1}\boldsymbol{b}$ の 1 組になるのです。

連立方程式 $A\boldsymbol{x}=\boldsymbol{b}$ の解が 1 組のみ $\Longleftrightarrow |A| \neq 0$

$|A|=0$ のときは、解の組が無数にあるか、そもそも解が存在しません。

連立方程式の中でも特に $A\boldsymbol{x}=\boldsymbol{o}$ の形のものについて。これは、同次連立方程式とも呼ばれ、右辺が全て 0 の連立方程式です。このとき、行列式 $|A|$ が 0 でないことと、解が $\boldsymbol{x}=\boldsymbol{o}$ 、つまり自明解のみになることは同値です。

同次連立方程式 $A\boldsymbol{x}=\boldsymbol{o}$ の解が自明解のみ $\Longleftrightarrow |A| \neq 0$

これは逆に言うと $A\boldsymbol{x}=\boldsymbol{o}$ の解が自明解のみならず自明解以外( $\boldsymbol{x}=\boldsymbol{o}$ 以外の解)も持つことと、 $|A|=0$ であることが同値ということでもあります。

同次連立方程式の解の数は、1 つ(自明解)or 無数(非自明解)のどちらかなのですが、行列式の値からそれを知ることができるのです。

なぜ上のようなことが言えるのかなど、詳しい内容はこちらのページをどうぞ。

【行列式編】連立方程式の解と行列式

おぐえもん.com

さいごに

これで、行列とは何？ってところから、行列式と連立方程式の関係までを扱いました。線形代数の前期試験ではおおよそこの範囲がメインになります。この記事で大枠を掴んだら、次は細かい証明などにも目を配り、最後に演習問題をガンガンといて知識と計算テクを定着させてください！

ちなみに、線形代数の試験でよく出る、行列式や逆行列を求める問題については、私が作成した自動計算機のドリル機能を通じて無限に演習できます。是非ともご活用ください ♪

行列式＆逆行列計算機（分数入出力対応！）

https://mat-det-inv.tools.oguemon.com/

最後まで読んでいただきありがとうございました！