【行列式編】逆行列の求め方を画像付きで解説！
大学1年生もバッチリ分かる線形代数入門

【行列式編】逆行列の求め方を画像付きで解説！

こんにちは、おぐえもん(@oguemon_com)です。

前回の記事では、行列（正方行列）の余因子について扱いました。今回は、行列式と余因子を用いて逆行列を求める方法について扱います。

余因子から逆行列を求める

逆行列の公式

余因子を用いると、逆行列は次の式で表されます。初見だとサッパリ分からないと思いますが、ご容赦ください m(_ _)m

逆行列の公式

正方行列AAが正則（逆行列をもつ）とき、逆行列A−1A^{-1}について、

A−1=1∣A∣t[Aij]=1∣A∣(A11A21⋯An1A12A22⋯An2⋮⋮⋱⋮A1nA2n⋯Ann)\begin{aligned} A^{-1} &=\frac{1}{|A|}{}^t[A_{ij}] \\ &=\frac{1}{|A|} \left( \begin{array}{cccc} A_{11} & A_{21} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{array} \right) \end{aligned}

ここで、AijA_{ij}は、ii行jj列成分の余因子である。

余因子で構成されている行列が転置の形をしている、つまり行と列が反転している点に注意です！（ii行jj列成分の余因子は、jj行ii列に置きましょう）

この行列にAAを掛け合わせてみましょう。1∣A∣\frac{1}{|A|}は一旦置いておき、行列部分のみの積を考えます。

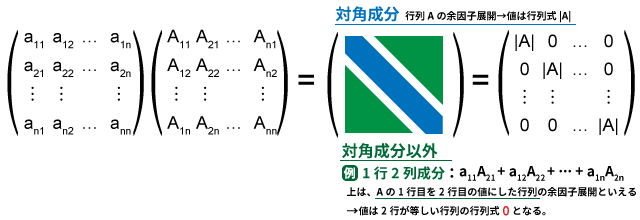
この時、積の対角成分は、行列AAに対する余因子展開の形になります。その値はズバリ余因子の元になった行列AAの行列式∣A∣|A|です。

一方で、対角でない成分は、「ある2つの行（or列）が等しい行列」に対する余因子展開の形になります。この値は、「2つの行（or列）が等しい行列」の行列式となります。行列式の性質から、値は0になります。

よって、この行列に1∣A∣\frac{1}{|A|}を掛け合わせると、単位行列EEになります。したがって、上に記した逆行列の公式がきちんと成立していることが分かります。

ちなみに、AAを掛け合わせる順番について言及しませんでしたが、どちらから掛け合わせても結果は単位行列になります（実際に確認してみよう！）。

行列が正則である条件

ここで、ある正方行列が正則である（逆行列）を持つための条件について触れます。

逆行列を持つか否かは、行列式の値を確認することで簡単に確かめられます。

行列が正則である条件

正方行列AAが正則である⟺∣A∣≠0\Longleftrightarrow |A| \neq 0

つまり、行列式が0であるかを確かめることで、逆行列を持つかが簡単にわかります！

理由は簡単。

正則⟹∣A∣≠0\Longrightarrow |A| \neq 0

AAが正則であるとき、A−1A^{-1}が存在するので、行列式の性質より、

∣A∣∣A−1∣=∣AA−1∣=∣E∣=1|A||A^{-1}|=|AA^{-1}|=|E|=1

が成り立ちます。

2つのスカラーの積が0でないということは、掛け合わせている2つの値は共に0でないので、∣A∣≠0|A| \neq 0が言えます。

∣A∣≠0⟹|A| \neq 0 \Longrightarrow正則

先ほど出てきた行列1∣A∣t[Aij]\frac{1}{|A|}{}^t[A_{ij}]が定義でき、これを左右のどちらから掛け合わせてもEEが導かれます。よって、逆行列を持つ、すなわち正則であると言えます。

逆行列を求める例

A=(121256134)A=\left( \begin{array}{ccc} 1 & 2 & 1 \\ 2 & 5 & 6 \\ 1 & 3 & 4 \end{array} \right)

の逆行列を求めましょう！

Step1:行列式を求める

そもそもこの行列が逆行列を持つのか確かめるため、まずは行列式を求めましょう。

どうせ後で余因子を全て求めることになることを見据えて、今回は、余因子展開を使って行列式を求めます。余因子展開の求め方については、前回の記事で扱いましたので、ここでは省略します。

さて、1行目の成分の余因子を全て求めてみました。

A11=2, A12=−2, A13=1A_{11}=2, \ A_{12}=-2, \ A_{13}=1

これより、

∣A∣=1∗2+2∗(−2)+1∗1=−1‾|A|=1*2+2*(-2)+1*1=\underline{-1}

です。ここで、∣A∣≠0|A| \neq 0が成り立つので、AAは逆行列を持つことがわかりました。

Step2:余因子を求める

残り6つの余因子を全て求めます！これだけでも、逆行列を導く面倒さが感じられると思います。

余因子を全て求めるとこんな感じ（行列の形で値を表現しています。）

(A11A12A13A21A22A23A31A32A33)=(2−21−53−17−41)\left( \begin{array}{ccc} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \\ \end{array} \right)=\left( \begin{array}{ccc} 2 & -2 & 1 \\ -5 & 3 & -1 \\ 7 & -4 & 1 \end{array} \right)

Step3:逆行列を求める

余因子を全て求める苦行を耐え抜いたら、逆行列は目の前です。上の公式にしたがって成分を置いていきましょう。

A−1=1−1(2−57−23−41−11)=(−25−72−34−11−1)\begin{aligned} A^{-1} &=\frac{1}{-1}\left( \begin{array}{ccc} 2 & -5 & 7 \\ -2 & 3 & -4 \\ 1 & -1 & 1 \end{array} \right) \\ &=\left( \begin{array}{ccc} -2 & 5 & -7 \\ 2 & -3 & 4 \\ -1 & 1 & -1 \end{array} \right) \end{aligned}

くぅ〜、疲れましたwこれにて計算終了ですw

逆行列を求める2つの方法

これで、逆行列の求め方を2つ紹介したことになります。

逆行列の求め方2つ

1つ目：行基本操作で単位行列を作る

ある行列AAと単位行列EEを左右に繋げた横長の行列[A E][A \ E]に対して行基本操作を繰り返し、左半分が単位行列になったら（[E P][E \ P]の形になったら）、右半分PPが逆行列です。

これは、行基本操作を経る過程で左半分に全部0の行が現れたりして、単位行列を作れないシチュエーションになった時点で逆行列を持たないことが分かります。

詳しくは以前の記事をご覧ください。

2つ目：逆行列の公式に当てはめる

今回の記事で扱った方法です。

A−1=1∣A∣t[Aij]A^{-1}=\frac{1}{|A|}{}^t[A_{ij}]

どちらの方法を用いてもきちんと逆行列（&逆行列の有無）が分かりますので、お好みに合わせて方法をお選びください〜

ちなみに、どちらの方法も行列の次数の3乗に比例して計算量が増えると言われています。サイズが大きくなると猛烈に計算が面倒になるのが行列あるあるです。

おわりに

最後に、行列の問題を「解く側」の人には関係ないかもしれないけど、作る人にとっては嬉しい性質があるのでご紹介します。

行列式が11または−1-1のどちらかである⟺\Longleftrightarrow逆行列の成分が全て整数

証明も比較的簡単です（ここでは省略します）。この性質を逆に言えば、行列式が±1\pm1以外の値ならば、成分に分数が含まれることになるということですね…

ただでさえ計算が面倒なのに、その過程で分数まで登場するなんてやっぱり行列は鬼です（・3・）

▲ トップへ戻る