【線形写像編】表現行列って何？定義と線形写像の関係を解説

2021年12月19日

こんにちは、おぐえもん(@oguemon_com)です。

前回は、線形写像とは何かを解説しました。あわせて「核」や「同型」といった関連ワードも紹介しています。

【線形写像編】線形写像って何？"核"や"同型"と一緒に解説

おぐえもん.com

今回は、ある線形写像で定められている対応付けの規則を表現する手法を解説します。その手法とは、行列を使うというものです。線形写像を行列と結びつけていいくのが今回の記事のキモです。

線形写像の表し方

表現行列

どんな線形写像 $f: \boldsymbol{a} \mapsto f(\boldsymbol{a})$ も、ある行列を用いて表現できます。この行列を、線形写像 $f$ に対応する表現行列といい、 $A_f$ などと記します。

表現行列

$V$ と $W$ はそれぞれ $n$ 次元と $m$ 次元の線形空間であり、 $V$ と $W$ の一組の基底をそれぞれ次の通り定める。

V\text{の基底} \Longrightarrow \boldsymbol{a}_1, \boldsymbol{a}_2, ..., \boldsymbol{a}_n \hspace{1cm} W\text{の基底} \Longrightarrow \boldsymbol{b}_1, \boldsymbol{b}_2, ..., \boldsymbol{b}_m

このとき、線形写像 $f: V \mapsto W$ について、

[f(\boldsymbol{a}_1) \quad f(\boldsymbol{a}_2) \quad ... \quad f(\boldsymbol{a}_n)] = [\boldsymbol{b}_1 \quad \boldsymbol{b}_2 \quad ... \quad \boldsymbol{b}_m]A_f

を満たす $m \times n$ 行列 $A_f$ を表現行列という。

$V$ のそれぞれの基底の $f$ による像 $f(\boldsymbol{a}_1)$ 〜 $f(\boldsymbol{a}_n)$ は、全て $W$ の要素なので、 $W$ の基底の一次結合で表現できます。

\begin{aligned} f(\boldsymbol{a}_1) &= a_{11}\boldsymbol{b}_1 + a_{21}\boldsymbol{b}_2 + ... + a_{m1}\boldsymbol{b}_m\\ f(\boldsymbol{a}_2) &= a_{12}\boldsymbol{b}_1 + a_{22}\boldsymbol{b}_2 + ... + a_{m2}\boldsymbol{b}_m\\ ...&=...\\ f(\boldsymbol{a}_n) &= a_{1n}\boldsymbol{b}_1 + a_{2n}\boldsymbol{b}_2 + ... + a_{mn}\boldsymbol{b}_m \end{aligned}

$mn$ 個の係数 $a_{11}$ 〜 $a_{mn}$ を行列の形にまとめたものが $A_f$ であり、 $n$ 個の式を行列の積の形に書き換えたものが、上に掲げた表現行列の定義式です。

行列 $A_f$ の各成分は、 $V,W$ の基底、写像 $f$ の組に応じて設定されます。そのため、写像が異なるときはもちろん、基底が変わっても行列 $A_f$ は変化します。

表現行列と任意要素の像

$V$ の要素 $\boldsymbol{a}$ の $f$ による像 $f(\boldsymbol{a})$ は、どんな要素であれ $f(\boldsymbol{a}_1)$ 〜 $f(\boldsymbol{a}_n)$ を用いて表現できます。

これは、 $V$ のどの要素も $V$ の基底の一次結合を用いて表現できることと、線形写像の性質を用いて確かめることができます。

$\boldsymbol{a} = \lambda_1\boldsymbol{a}_1 + \lambda_2\boldsymbol{a}_2 + ... + \lambda_n\boldsymbol{a}_n$ （ $\lambda_1$ 〜 $\lambda_n$ はスカラー）とすると、

\begin{aligned} f(\boldsymbol{a}) &= f(\lambda_1\boldsymbol{a}_1 + \lambda_2\boldsymbol{a}_2 + ... + \lambda_n\boldsymbol{a}_n)\\ &= \lambda_1f(\boldsymbol{a}_1) + \lambda_2f(\boldsymbol{a}_2) + ... + \lambda_nf(\boldsymbol{a}_n) \end{aligned}

これより、 $f(\boldsymbol{a}_1)$ 〜 $f(\boldsymbol{a}_n)$ さえ定めれば線形写像 $f$ の像を網羅できます。したがって、線形写像は全て $mn$ 個の数 $a_{11}$ 〜 $a_{mn}$ で表現できるのです。

表現行列と成分

線形空間の要素を書くとき、基底を全て書くのではなく、一次結合の各係数のみを抜き出した成分表記で書くと楽です。成分表記で変換後の成分を表すとき、表現行列が活きてきます。

$V$ の任意の要素を $\boldsymbol{x}=x_1\boldsymbol{a}_1+...+x_n\boldsymbol{a}_n$ 、

そのある写像を $f(\boldsymbol{x})=y_1\boldsymbol{b}_1+...+y_m\boldsymbol{b}_m$ とする。

$A_f$ が $f$ に対応する表現行列の場合、 $\boldsymbol{x}$ と $f(\boldsymbol{x})$ の成分間に次の関係がある。

\begin{pmatrix} y_1 \\ \vdots \\ y_m \end{pmatrix} = A_f \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}

つまり、成分を縦に並べた列ベクトルを用いて写像を考える場合、対応元の要素の成分に対して表現行列を左から掛けるだけで、対応する要素の成分を導けます。

この性質は、簡単な計算で導けます。

\begin{aligned} f(\boldsymbol{x}) &=f(x_1\boldsymbol{a}_1+...+x_n\boldsymbol{a}_n) \\ &=x_1f(\boldsymbol{a}_1)+...+x_nf(\boldsymbol{a}_n) \\ &=x_1\sum_{i=1}^{m}a_{i1}\boldsymbol{b}_i+...+x_n\sum_{i=1}^{m}a_{in}\boldsymbol{b}_i \\ &=(\sum_{j=1}^{n}x_ja_{1j})\boldsymbol{b}_1+...+(\sum_{j=1}^{n}x_ja_{mj})\boldsymbol{b}_m \end{aligned}

$\boldsymbol{b}_1$ 〜 $\boldsymbol{b}_m$ は基底であるゆえに一次独立なので、 $f(\boldsymbol{x})=y_1\boldsymbol{b}_1+...+y_m\boldsymbol{b}_m$ と係数比較をして次式が成り立ちます。

\begin{aligned} y_1 &= \sum_{j=1}^{n}x_ja_{1j} = x_1a_{11} + x_2a_{12} + ... + x_na_{1n} \\ y_2 &= \sum_{j=1}^{n}x_ja_{2j} = x_1a_{21} + x_2a_{22} + ... + x_na_{2n} \\ ... &= ... \\ y_m &= \sum_{j=1}^{n}x_ja_{mj} = x_1a_{m1} + x_2a_{m2} + ... + x_na_{mn} \end{aligned}

よって、 $A_f=[a_{ij}]$ として次式が成立します。

\begin{pmatrix} y_1 \\ \vdots \\ y_m \end{pmatrix} = A_f \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}

表現行列と線形写像の演算

線形写像の演算は、そのまま表現行列の演算と対応します。

線形写像の和とスカラー倍

2つの写像 $f$ と $g$ はともに $V \rightarrow W$ の線形写像とし、 $\lambda$ と $\mu$ はスカラーとします。このとき、集合 $V$ の要素 $\boldsymbol{x}$ に、 $\lambda f(\boldsymbol{x})+ \mu g(\boldsymbol{x})$ という要素を対応させる写像もまた $V \rightarrow W$ の線形写像です。この写像を $\lambda f+ \mu g$ と書きます。

$f$ と $g$ と $\lambda f+ \mu g$ は、表現行列について次の関係があります。

$f$ 、 $g$ 、 $\lambda f+ \mu g$ の表現行列をそれぞれ $A_f$ 、 $A_g$ 、 $A_{\lambda f+ \mu g}$ とするとき、次式が成立する。

A_{\lambda f+ \mu g} = \lambda A_f+ \mu A_g

上記の表現により、和について $A_{f+g} = A_f+A_g$ が成立することと、スカラー倍について $A_{\lambda f} = \lambda A_f$ が成立することを同時に表せます。（前者は $\lambda=\mu=1$ のとき、後者は $\mu=0$ のとき）

線形写像の合成

線形写像 $f:S \rightarrow T$ と $g:T \rightarrow U$ に対して、合成写像 $g \circ f: S \rightarrow U$ もまた線形写像です。

このとき、 $f$ と $g$ と $g \circ f$ は、表現行列について次の関係があります。

$f$ 、 $g$ 、 $g \circ f$ の表現行列をそれぞれ $A_f$ 、 $A_g$ 、 $A_{g \circ f}$ とするとき、次式が成立する。

A_{g \circ f} = A_g A_f

基底を変換したときの表現行列の変化

基底をある行列で別の組み合わせに変換したとき、対応する表現行列はある規則にしたがって変換します。

線形空間 $V$ と $W$ のそれぞれの基底 $\boldsymbol{a}_1, ..., \boldsymbol{a}_n$ と $\boldsymbol{b}_1, ..., \boldsymbol{b}_m$ は、それぞれ正則行列 $P$ と $Q$ を用いて、別の基底 $\boldsymbol{a}'_1, ..., \boldsymbol{a}'_n$ と $\boldsymbol{b}'_1, ..., \boldsymbol{b}'_m$ に変換されるものとする。

このとき、線形写像 $f: V \rightarrow W$ の表現行列 $A_f$ は次式を満たす行列 $A'$ に置き換わる。

A' = Q^{-1}AP

特に、 $V=W$ のとき（つまり線形変換のとき）は次式のようになります。

A'=P^{-1}AP

この右辺、固有値編で度々出てきた形ですよね。後ほど、線形変換と固有値を絡めた議論でこの公式が登場します。

$A' = Q^{-1}AP$ の成立は、次の方法で導けます。まずは前提の整理です。

次に、上の式を用いて、 $f(\boldsymbol{a}'_i)$ を2通りで変形します。

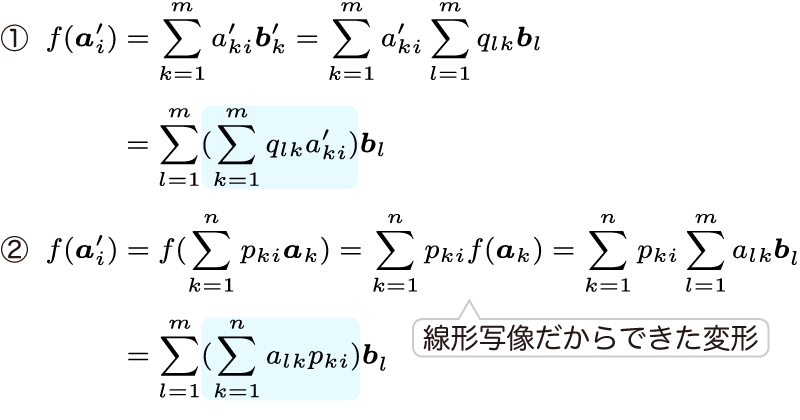
$\boldsymbol{b}_1,...,\boldsymbol{b}_n$ は基底なので一次独立です。よって、両者の係数を比較して、

\sum_{k=1}^{m} q_{lk} a'_{ki} = \sum_{k=1}^{n} a_{lk} p_{ki}

左辺は積 $QA'$ の $(l, i)$ 成分で、右辺は積 $AP$ の $(l, i)$ 成分です。これが各成分に対応することから $QA'=AP$ が成立するので、両辺に $Q^{-1}$ を左から掛けて $A' = Q^{-1}AP$ です。