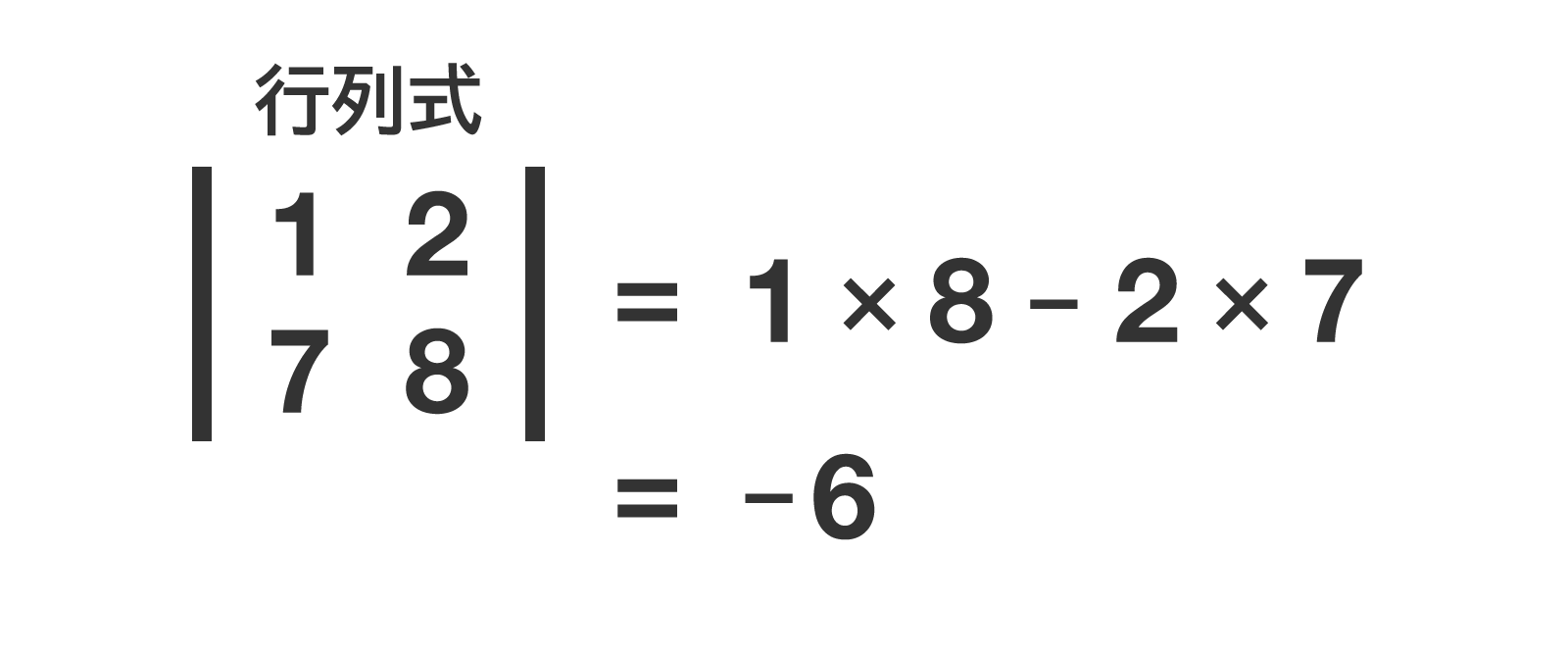こんにちは、おぐえもん(@oguemon_com)です。
さて、ある行列の逆行列を求める公式が成り立つ理由を説明する際、「余因子」というものを活用します。今回は余因子について解説し、後半では余因子を使った重要な等式である「余因子展開」に触れます。
余因子について
余因子ってなに?
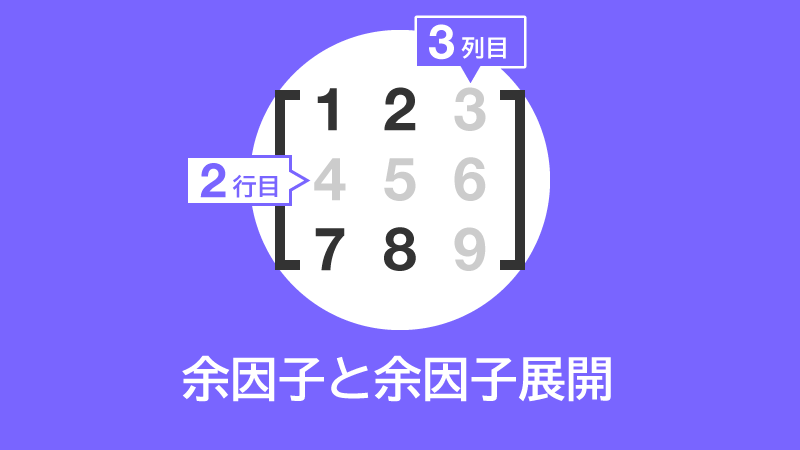
簡単に言えば、ある行列の行と列を 1 つずつカットして残った一回り小さい行列の行列式に、正負の符号を加えたものです。直感的に表現したのが次の画像です。
正方行列Aのi行目とj列目をカットして作る余因子を(i,j)成分の余因子と呼び、Aijと記します。
余因子の作り方
余因子の作り方を分かりやすく学ぶために、実際に一緒に作ってみましょう!例として、次の行列について「2 行 3 列成分」の余因子を求めてみます。
A=147258369
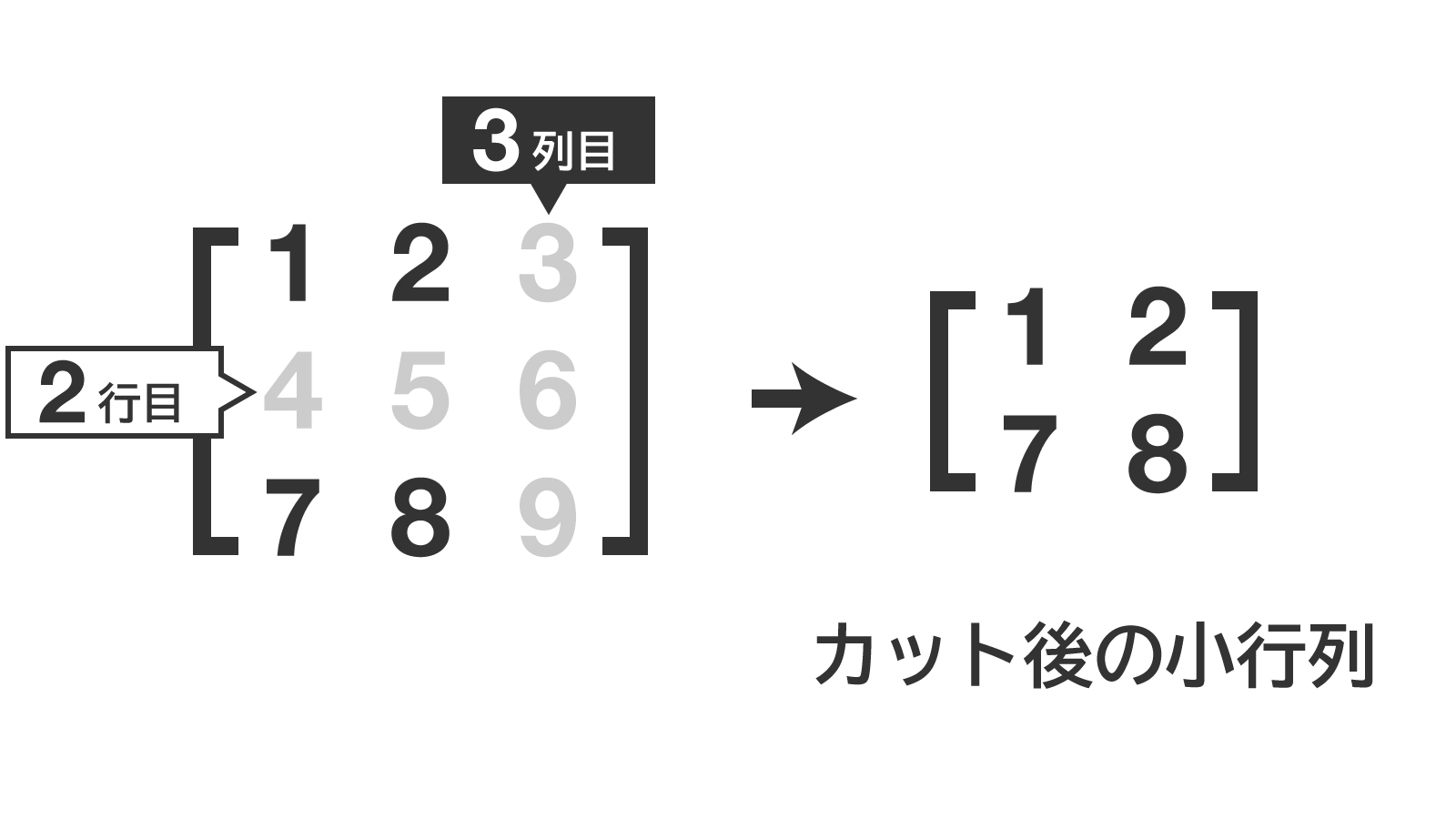
ステップ1|「2行目」と「3列目」を抜き去る。
ステップ2|小行列の行列式を求める。
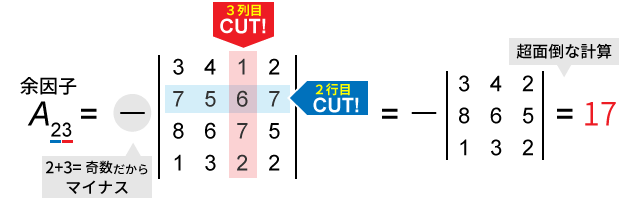
ステップ3|行列式に符号をつける。
行番号と列番号の和が偶数ならば「1」を、奇数ならば「-1」を掛け合わせます。
これで、余因子A23を導出できました。計算こそ面倒ですが、ルール自体は割とシンプルなのがお判りいただけましたか?
余因子の作り方(一般化)
余因子の作り方を一般化して表すと次の通りです。まあ、やってることは方法は上とほぼ同じです(笑)
余因子の作り方
正方行列Aから(i,j)成分の余因子Aijを作りたい!
- 行列Aからi行とj列を抜き去る。
- その行列の行列式を計算する。(これをDijと書きます)
- 求めた行列式に対して、行番号と列番号の和が偶数ならば「プラス」を、奇数ならば「マイナス」をつけて完成!
Aij={Dij−Dij(i+j=偶数)(i+j=奇数)
そもそも、行列式がよく分からない人は次のページを参考にしてください。
行列式って何?
おぐえもん.com
ちなみに、最後に加える符号は、成分の場所に応じて次のようになっています。これは覚えておくと便利です。
+−+⋮−+−⋮+−+⋮⋯⋯⋯⋱
余因子展開
余因子が持つ重要な性質
(i,j)成分の余因子Aijと、(i,j)成分そのものaijを掛け合わせた積aijAijを考えます。
この「成分 × 余因子」を、同じ行(または列)の全ての成分で足し合わせると、もとの行列Aの行列式と等しくなります。
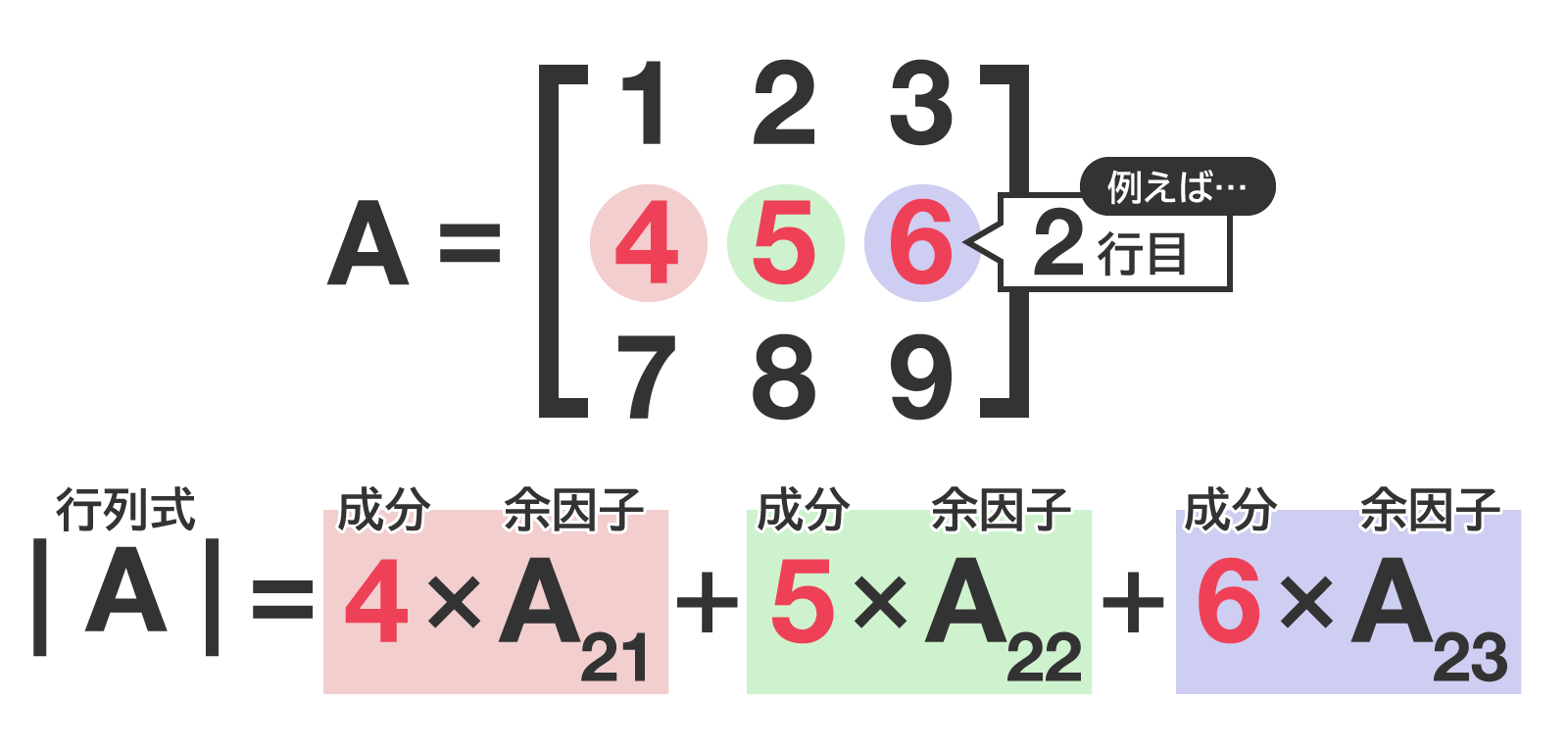
つまり、行列式は、「成分 × 余因子」同士の足し算の形に展開できるわけです。この展開を余因子展開と呼びます。一般的な形で書くと次の通り。
余因子展開
行列Aに対する(i,j)成分の余因子をAijとする。
この時、行列Aのそれぞれの行について次の式が成り立つ。
∣A∣=ai1Ai1+ai2Ai2+⋯+ainAin
同じく、それぞれの列について次の式が成り立つ。
∣A∣=a1jA1j+a2jA2j+⋯+anjAnj
この性質が成り立つ理由は複雑で、そのうえ話が長くなるため割愛します。多分講義で先生が一生懸命に証明してくれると思うんで頑張って板書してください。
余因子展開って何が嬉しい?
みなさんが思う通り、余因子展開は、超面倒な計算を伴う性質です。よって、これを用いて行列式を求めることはほとんどありません(ただし、成分に 0 が多い行列を扱う時はこの限りではありません)。
が、この性質は逆行列の公式を導く上で重要な役割を果たします。なので線形代数の講義ではほぼ絶対に取り上げられるのです。
【行列式編】逆行列の求め方を画像付きで解説!
おぐえもん.com
初学者のみなさんは、ひとまず余因子展開は逆行列を求めるための前座と捉えておけば OK です!
余因子展開の例
実際に余因子展開ができることを確かめてみましょう。
ここでは「余因子の例」で扱ったものと同じ行列を用います。
A=147258369
先ほどの例から、2行3列成分の余因子A23が6であると分かりました。そこで、今回は2行目の成分の余因子を用いた次の余因子展開の成立を確かめます。
∣A∣=a21A21+a22A22+a23A23
まず、2行1列成分の余因子A21を求めます。これは、
D21=2839=−6
かつ、「2+1=3(奇数)」より、A21=6です。
同様にすると、2行2列成分の余因子A22は、−12であることが分かります。
2行3列成分の余因子A23は前半で求めた通り6ですよね?
さて、材料が揃ったので、a21A21+a22A22+a23A23を計算します。
a21A21+a22A22+a23A23=4∗6+5∗(−12)+6∗6=0
これがもとの行列の行列式∣A∣と同じであることを示すため、∣A∣を頑張って計算します(途中式は無視して構いません)。
∣A∣===1∗5∗9+2∗6∗7∗+3∗4∗8−3∗5∗7−2∗4∗9−1∗6∗845+84+96−105−72−480
先ほどの結果と同じく「0」が導かれました。よって、もとの行列式と同じであること、つまり余因子展開が成立することが確かめられました。
おわり
今回は逆行列を求めるために用いる「余因子」について扱いました。次回は、逆行列の一般的な求め方について扱いたいと思います!
【行列式編】逆行列の求め方を画像付きで解説!
おぐえもん.com