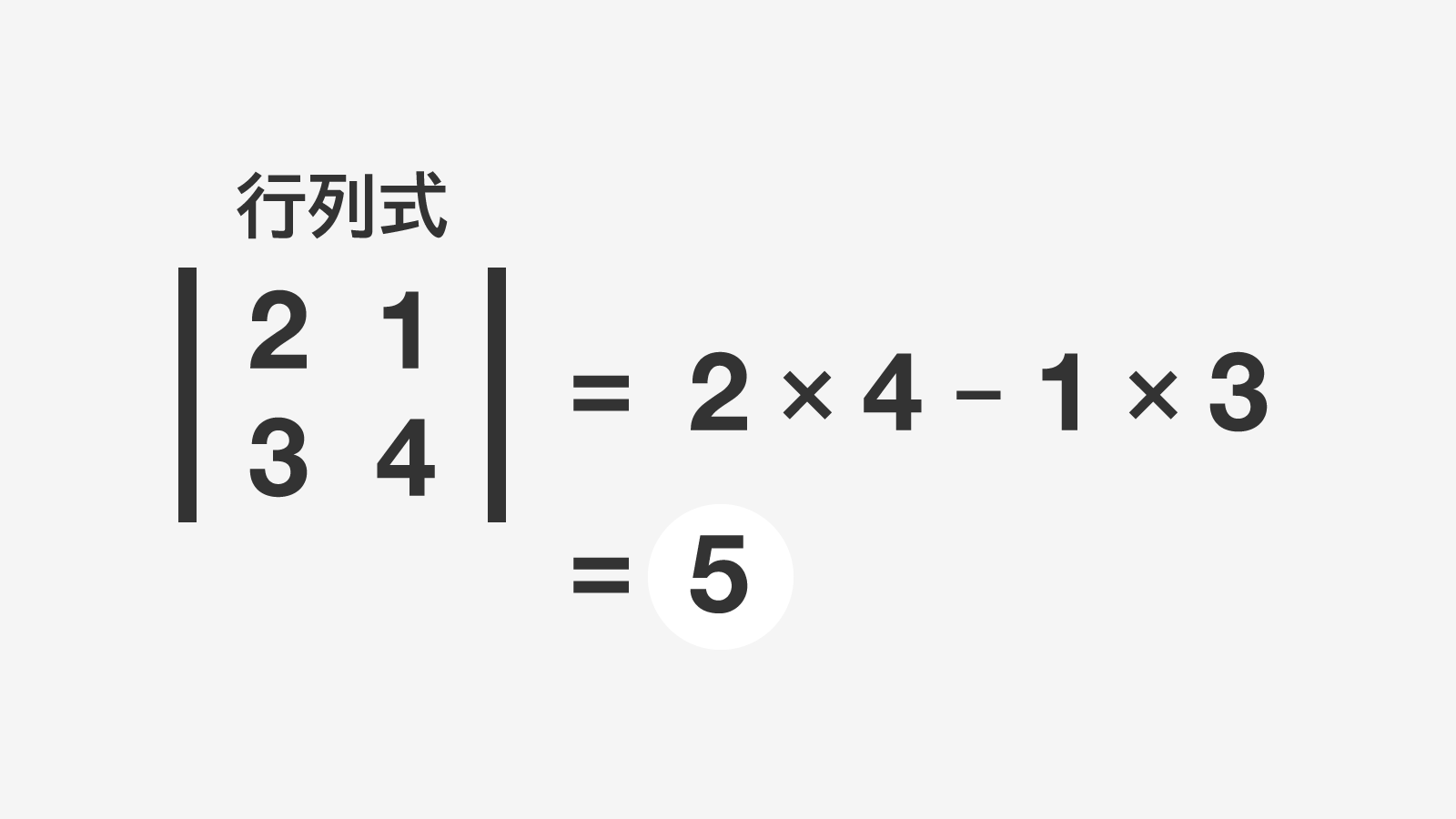行列式って何？

2017年2月7日作成2019年10月5日更新

こんにちは、おぐえもん(@oguemon_com)です。

今回からは、行列式や逆行列についてのお話を進めます。連立方程式のお話については【連立方程式編】消去法と階段行列以降の記事をご覧ください。

さて、早速はじめましょう！！

行列式とは？

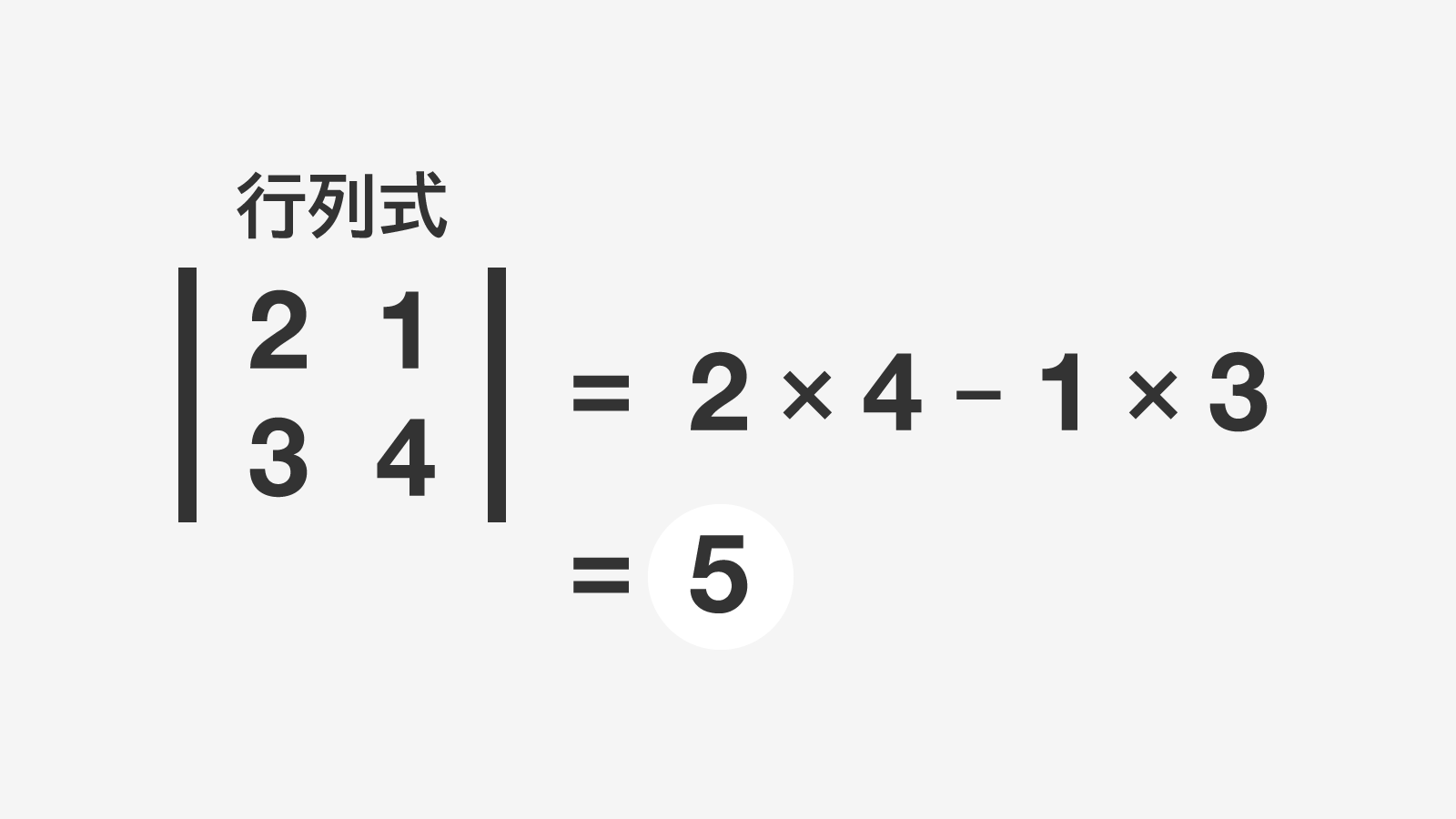
行列式は、行列の特徴を表す指標の 1 つです。行列式なんて言いますが、方程式などではなく、スカラーです。つまり、「1」「3」みたいな値をとります。

行列式の定義は結構複雑です。この記事では 2 次と 3 次の行列の例に留め、一般的な定義については次回以降の記事で扱います。

行列式が最も活躍するのは、逆行列を導出する場面です。

逆行列とは、ある行列にかけることで、その行列を単位行列にしてしまう行列のことです。逆行列は、連立 1 次方程式を一瞬で解くことを可能にするなど、行列計算の上で非常に有益かつ重要な力を有します。

行列式は、逆行列の導出に必要な値です。そして、行列式の値から、逆行列がそもそも存在するのかを確認することができます。

おぐえもん

行列式の値が0か否かで、逆行列を持たないかどうかが分かります。

行列 $A$ の行列式は、 $|A|$ や ${\rm det}(A)$ と表します。「det」は、行列式の英語に当たる"determinant"に由来します。

どちらを使用しても構いませんが、以降では、 $|A|$ の方を使用します。

まず、行列式は正方行列に対してのみ定義されます。よって、以降では基本的に正方行列のみ扱うこととします。

行列式の定義は、一般的な $n$ 行 $n$ 列行列に対して説明するとかなり複雑になるので、今後いくつかの記事を経て展開することになります。

今回は、'さわり'なので、定義が比較的簡単である 2 次正方行列と 3 次正方行列の場合について説明します。

かなり簡単です。

A=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)

について、

|A|=a_{11}a_{22}-a_{12}a_{21}

つまり、「（左上×右下）-（右上×左下）」ですね。

【例】次の行列の行列式を求めます。

B=\left( \begin{array}{cc} 3 & 2 \\ 5 & 4 \end{array} \right)

について、 $|B|=3*4-2*5=12-10=\underline{2}$ です。

次数が1つ増えただけなのに、かなり複雑になります…

A=\left( \begin{array}{ccc} a*{11} & a*{12} & a\_{13} \\ a*{21} & a*{22} & a\_{23} \\ a*{31} & a*{32} & a\_{33} \end{array} \right)

について、

\begin{array}{rr} |A|=&a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\ &-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32} \end{array}

式で表すと複雑すぎるので、次の図で表現される場合も多々あります。

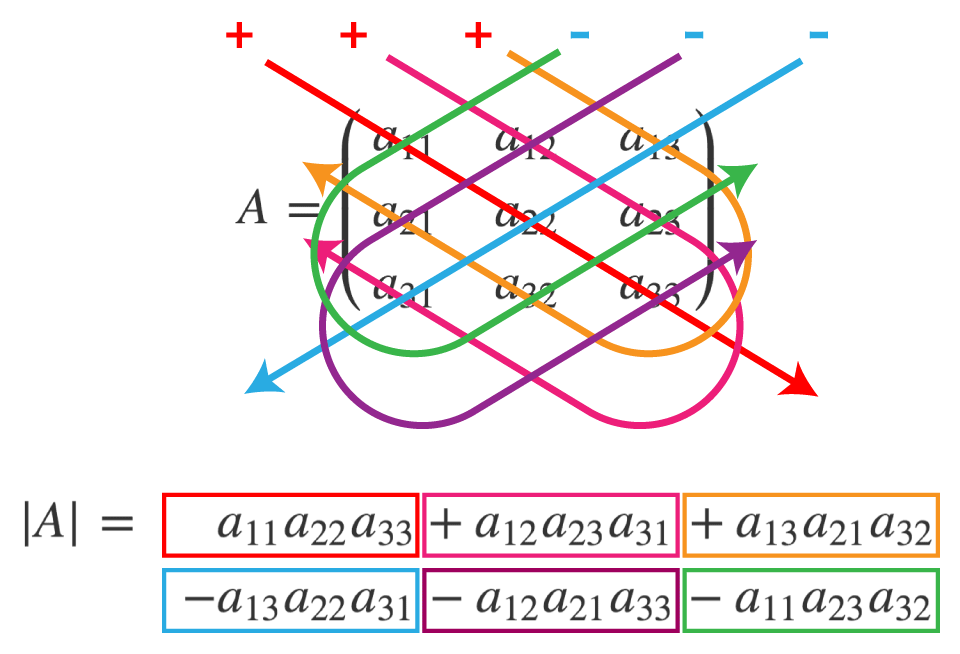
【例】次の行列の行列式を求めます。

C=\left( \begin{array}{ccc} 1 & 3 & 2 \\ 5 & 4 & 6 \\ 8 & 9 & 7 \end{array} \right)

について、

\begin{aligned} |C| &=(1*4*7)+(3*6*8)+(2*5*9)\\ & -(2*4*8)-(3*5*7)-(1*6*9)\\ &=28+144+90-64-105-54\\ &=\underline{39} \end{aligned}

と定義されます。

今回は、行列式の概要と、簡単な行列に対する行列式の定義について扱いました。次回以降では、行列式を導くために必要な「置換」という概念などに関する説明を進めることで、 $n$ 行 $n$ 列行列の行列式の定義に迫ります。