【固有値編】固有値と固有ベクトルって何？

こんにちは、おぐえもん(@oguemon_com)です。

今回から固有値や固有ベクトルに焦点を当てたシリーズを始めます！今までの記事を読みたい方は、こちらのカテゴリトップページへお進みください。

初回らしく、そもそも固有値や固有ベクトルとはどんなものなのかを簡単に説明します。

固有値と固有ベクトルって何？

線形代数には、下の式のように、あるベクトル$\boldsymbol{x}$に対して"正方"行列$A$を左から掛けることで、別のベクトルに変換する方法がよく使われます。

これを行列$A$による線形変換と呼びます。（記事の下部で具体例を挙げています）

線形変換をすると、ほとんどのベクトルは行列$A$との掛け算に基づいて別のベクトルに変化します。しかし、中には、ベクトルの大きさこそ変わるけど、向きに一切の変化が生じないベクトルが存在する場合があります。つまり、下の式のように、ベクトル$A\boldsymbol{x}$が、同じベクトル$\boldsymbol{x}$のスカラー倍の形で書けることがあるんです。

ここで、向きが変わらない特別なベクトル$\boldsymbol{x}$のことを固有ベクトルと呼び、変換後におけるベクトルの大きさの変化率$\lambda$のことを固有値と呼びます。固有値と固有ベクトルはセットになっていて、ある行列$A$に対していくつかのセットがある場合がほとんどです。

ちなみに、上の式「$A\boldsymbol{x}=\lambda \boldsymbol{x}$」において、$\boldsymbol{x}$が零ベクトルならばどんな場合でも成り立ちますが、零ベクトルは固有ベクトルと見なしません。

これって何に役立つの

固有値と固有ベクトルは、ある行列を用いた線形変換の特徴を示す指標の 1 つです。線形代数で習う事柄の中でも固有値＆固有ベクトルは特に世の中でたくさん使われていて、利用例を挙げると

など枚挙にいとまがありません。

簡単な具体例

簡単な例として、次に掲げる 2 次元の正方行列$A$を考えます。

まずは、なんの変哲もないベクトル$\boldsymbol{x}=\left(\begin{array}{c}2 \\ 1\end{array}\right)$を線形変換します。

このように全然違う向きのベクトルが生成されました。固有ベクトル以外の大多数のベクトルは、線形変換を通じてこのような挙動をします。

ところがどっこい、固有ベクトルを与えるとどうでしょう。試しに$A$の固有ベクトルである$\boldsymbol{x}=\left(\begin{array}{c}-3 \\ 2\end{array}\right)$を線形変換します。

なんということでしょう。変換後のベクトルは、変換前と向きが変わらないではありませんか。長さは 3 倍になりましたが、この変化率「3」は行列$A$の固有値の 1 つとなります。

他にも何個かのベクトルについて線形変換を適用してみた結果を２次元平面にまとめてみました。ピンクのベクトルが固有ベクトルで、それ以外は固有ベクトルでありません。両者の違いを体感してみてください。

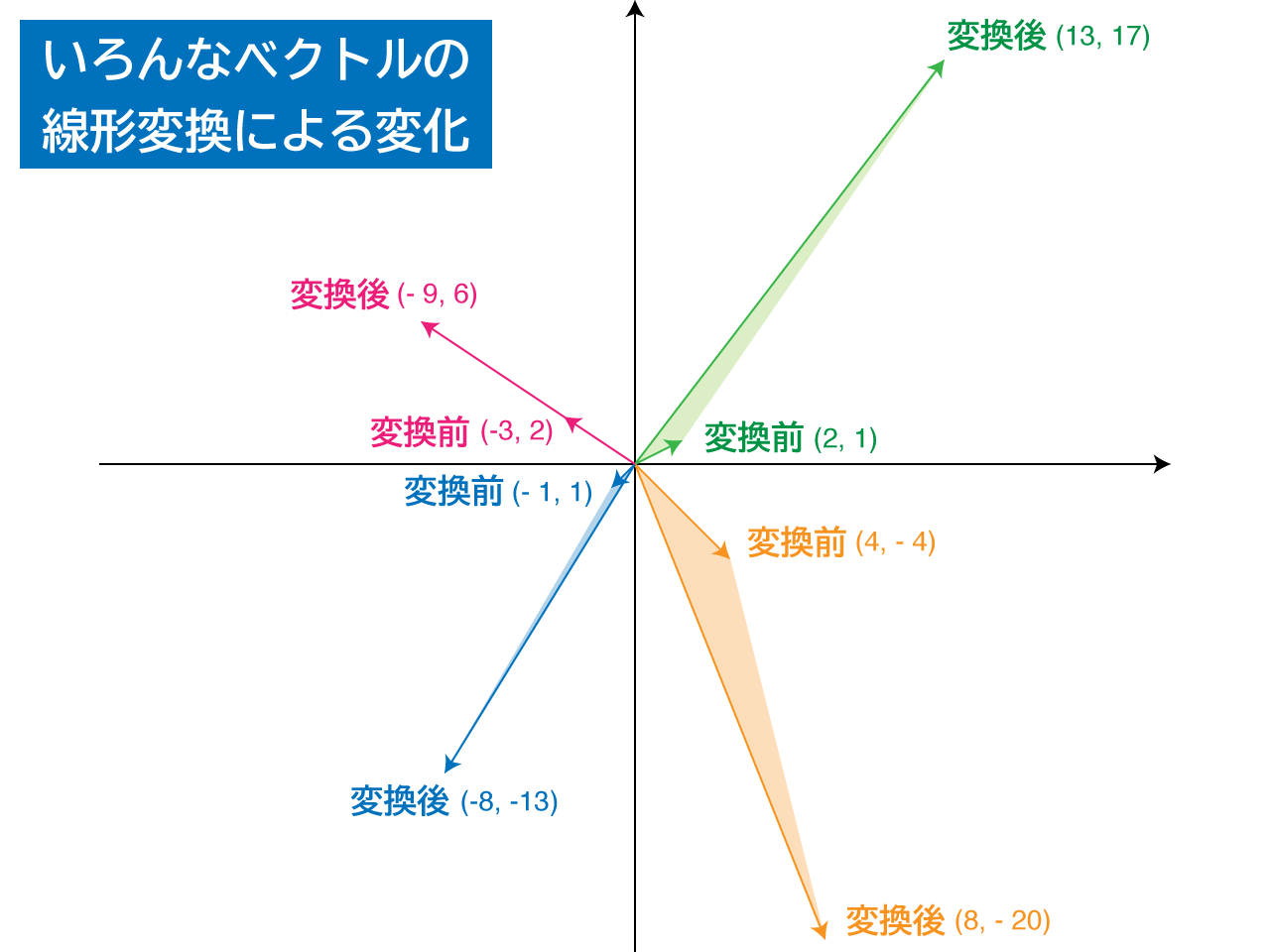
ちなみに、$\boldsymbol{x}=\left(\begin{array}{c}-3 \\ 2\end{array}\right)$と異なる向きをもつ他の固有ベクトルを探すことで、行列$A$の固有値をもう一つ見つけることができます。余力のある方は頑張って見つけてみてください！（多分途方に暮れると思いますが…）

この行列の他の固有値＆固有ベクトルを求める方法は、次の記事でご紹介します。

おわりに

今回は、固有値と固有ベクトルの基礎を学びました。

次回の記事では、固有値＆固有ベクトルの手っ取り早い求め方を解説します。