【ベクトル編】3次元空間と位置ベクトルと座標系

こんにちは、おぐえもん(@oguemon_com)です。

前回の記事では、ベクトルの内積と外積について解説しました！

今回は、打って変わって「座標 × ベクトル」をテーマに掲げ、馴染み深い 3 次元座標をベクトルを使って作る方法について解説します。

原点と位置ベクトル

3 次元空間について色々考えるとき、ある「点」の位置を確実な方法で表現したくなります。

しかし、何もない空間の中で、ここがどこなのかを表現するのは簡単じゃありません。

例えば宇宙の中で、地球がどこにあるのか厳密に説明できませんもんね。

数学では、そのような問題に対して、「位置表現の基点を設定する」という解決策を見出しました。

絶対に動かない点（原点 O）を勝手に用意して、全ての点を「原点 O からの位置」で表現すると確実です。

ベクトルを 3 次元空間に持ち込むと、「ある点 P」の位置を、基点 O から点 P へ伸びるベクトル$\vec{OP}$で表現できます。

このように、ある点の位置を表現するベクトルを位置ベクトルと呼びます。

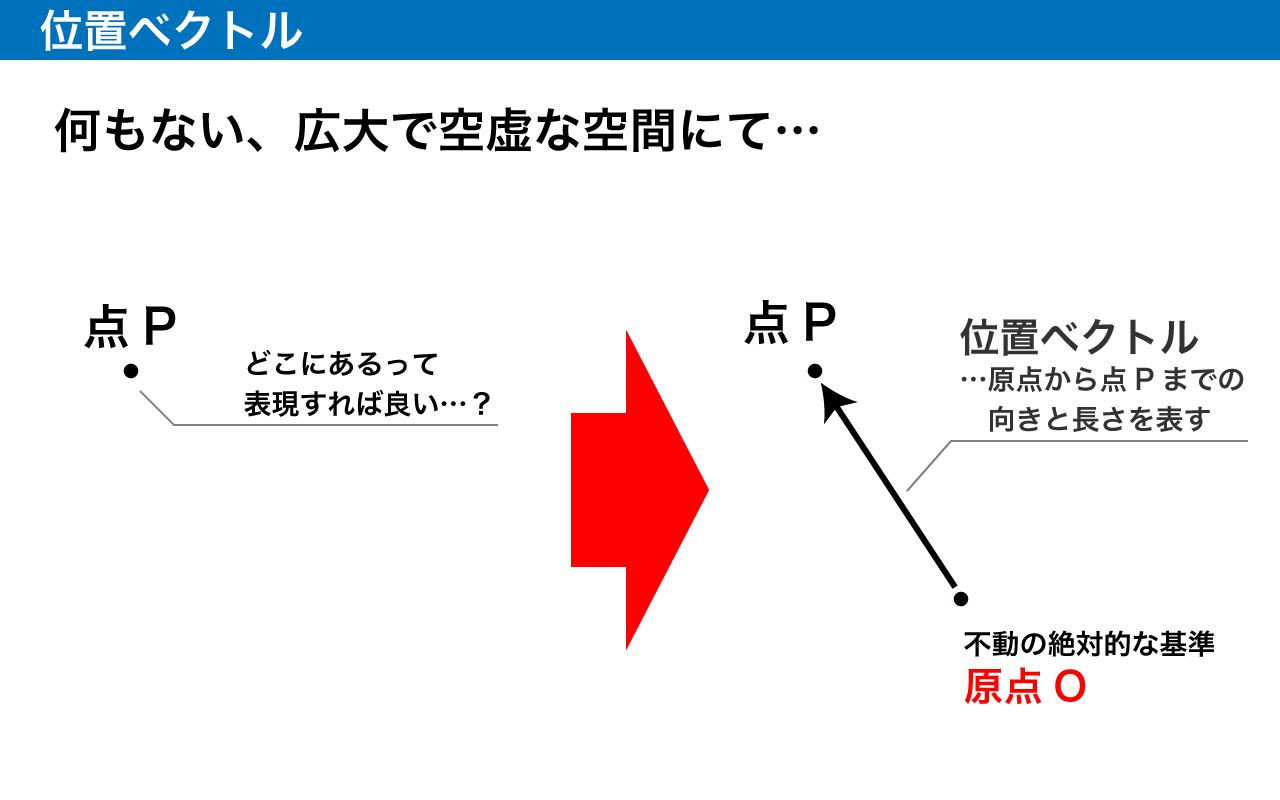
位置ベクトルは、原点から「どの向き」に「どの長さ」進めば点に到着するかを表します。ですので、普通のベクトルと同じく向きと長さの情報しか持たないのですがその役割をしっかり果たしてくれます。

全部の点を何本かの共通するベクトルで表したい！（基本ベクトル）

これで、3 次元空間上にある全ての点の位置を「原点＋ 1 本のベクトル」で表現できるようになりました。

しかし、これではまだまだ不便です。というのも、「位置の比較」が難しいのですよね。

異なる位置にある点にそれぞれ対応する位置ベクトルは、向きも長さも様々です。頑張れば比較できなくもないですが、もっと簡単にできそうです。

簡単にする方法の 1 つに、「全ての点の位置を、少ないベクトルのスカラー倍と和で表現する」ことがあります。

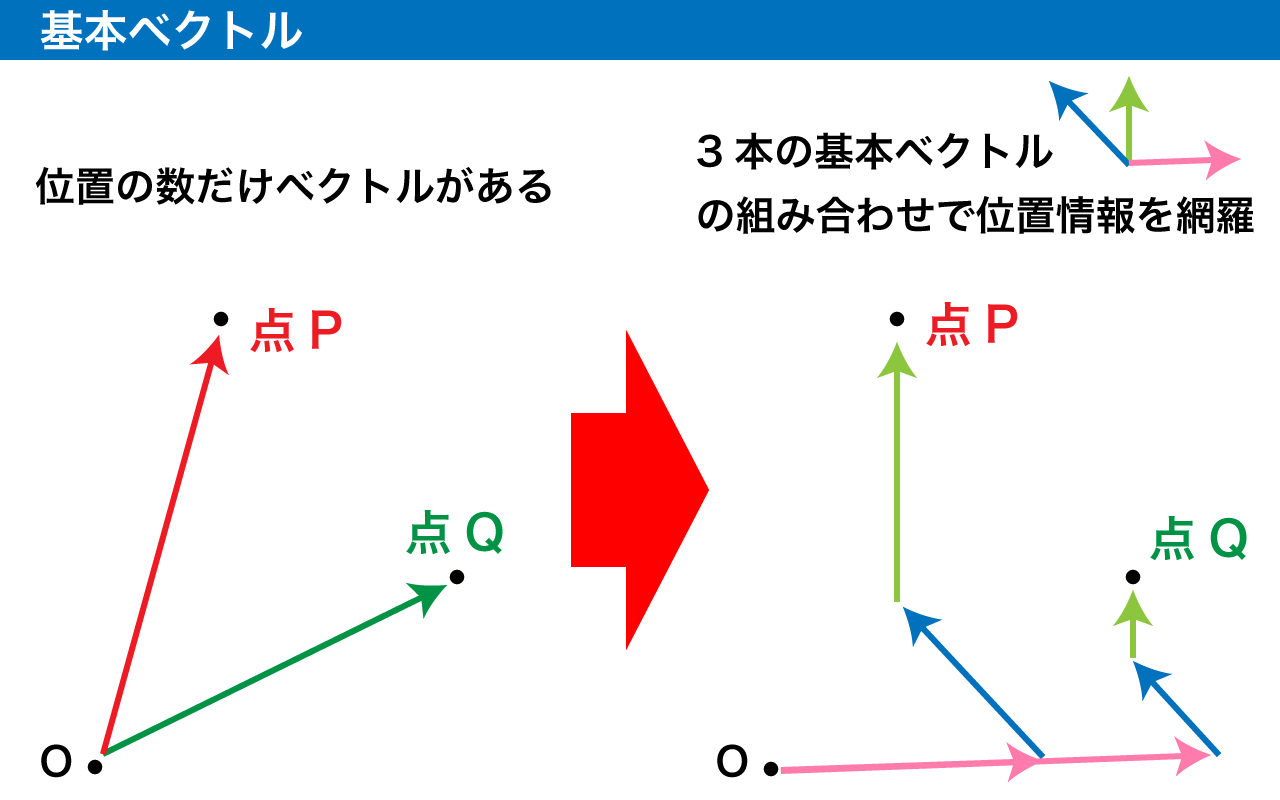
あらかじめ数本のベクトル$\vec{a},\vec{b},\vec{c}$を用意しておいて、全部の点の位置ベクトルをそのベクトルの組み合わせ$x\vec{a}+y\vec{b}+z\vec{c}$で表現すると、3 つの実数$(x,y,z)$の組み合わせだけで位置を表現できて便利です。

3 次元空間上の点の位置は、「3 本のベクトル」を都合よく選ぶことで全ての位置を余すことなく表現できます。

そのようなベクトル$\vec{a},\vec{b},\vec{c}$を基本ベクトルと呼び、原点と基本ベクトルの組み合わせ$\{O:\vec{a},\vec{b},\vec{c}\}$を座標系と言います。

ちなみに、点 P の位置ベクトル$\vec{OP}$を表現する 3 つの実数の組み合わせ、$(x,y,z)$を、P の成分と呼びます。

高校までで習ってきた「xyz 座標空間」なんてものは、まさにこの考え方に基づいて生み出された概念です。

1次独立と1次従属

3 次元空間上の全ての位置は「3 本のベクトル」で表現できると言いましたが、これには「都合よく選ぶことで」という条件がついています。適当に 3 本選べば良いってわけじゃないんですよね。

3 本選んでもダメな例が、「3 本のうち 1 本が他の 2 本のスカラー倍と足し算で表現できる」とき。これって、点の位置を実質 2 本のベクトルで表現することになるので、2 本のベクトルが織りなす平面上の点にしか対応できません。ちなみに、このような 3 つのベクトルは1 次従属と言います。詳しくは昔の記事に書いてます。

逆に言えば、1 次従属でない 3 本のベクトルを持ってこれば良いのです。このような 3 本のベクトルを1 次独立と言います。

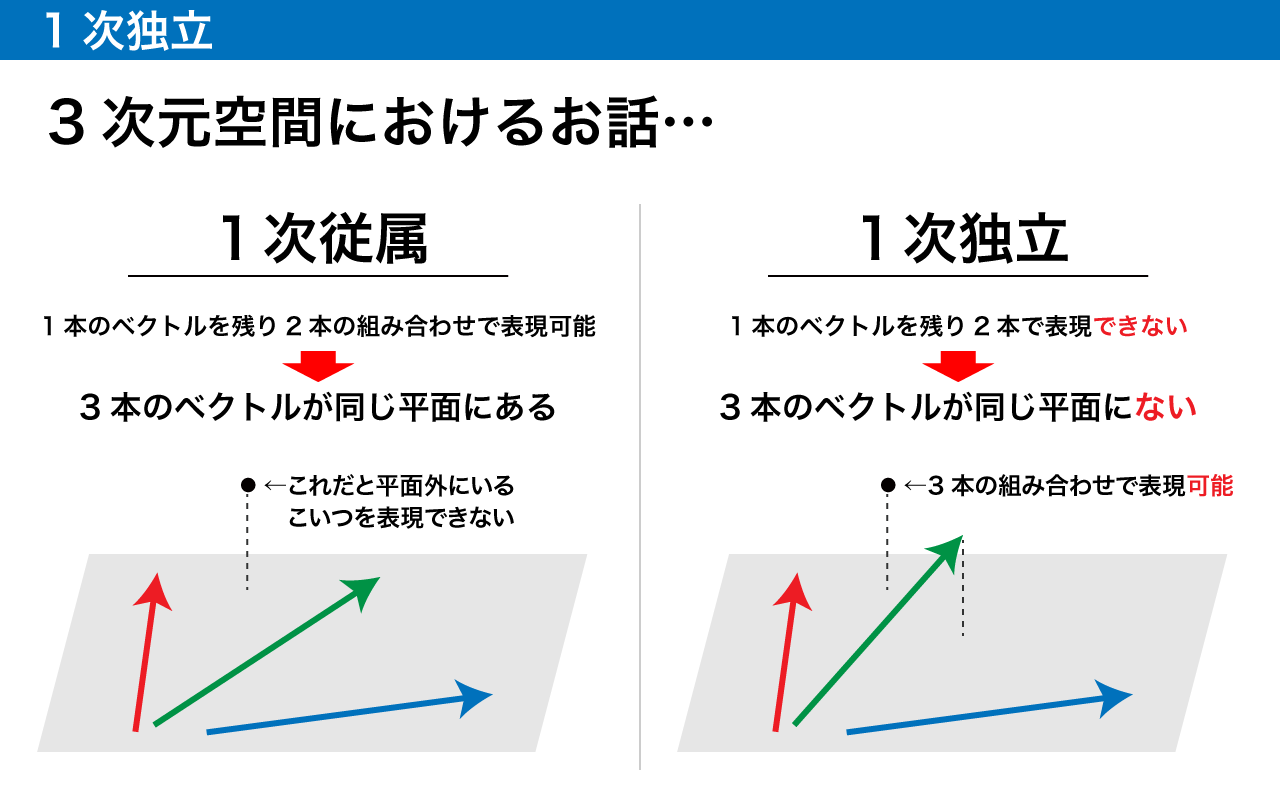
1 次独立は、「3 本の中のどの 1 本も、他の 2 本のスカラー倍と足し算で表現できない」ことを言うのですが、これを数式にすると次のようになります。

ちなみに、2 次元平面だったら、1 次独立な 2 本のベクトルを用意することで、平面上の全ての位置を表現できるようになります。

直交座標系

これで、少ない本数のベクトルで簡単に位置を表現できるようになりました。けれど、まだなんか物足りませんよね？

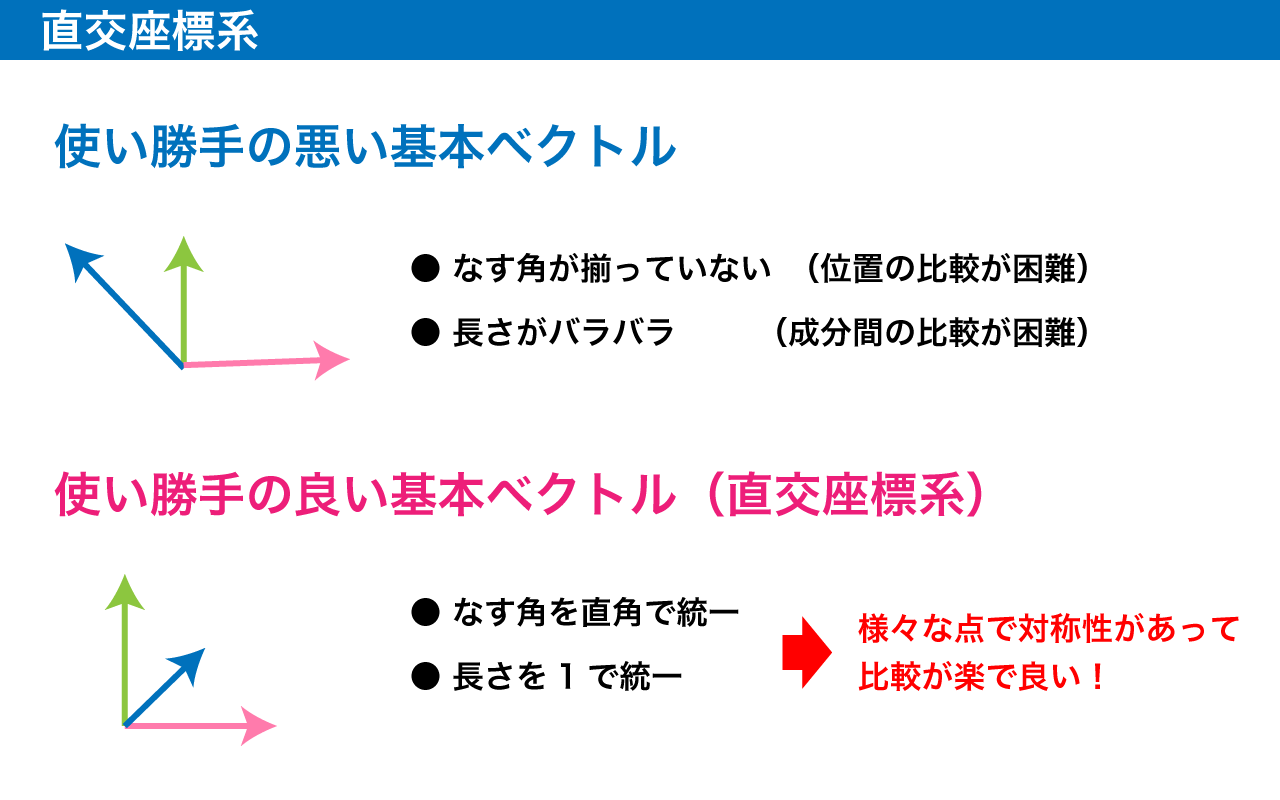
そうです、3 本のベクトルはあっちこっち向いてるわけです。ベクトルが中途半端な角度をなしている状態は、使いやすさや分かりやすさを考えるともう一声といった感じです。

さらに、ベクトルの長さがバラバラだと、成分の値の大小をどう捉えれば良いのかもよく分かりません。

そこで、「互いに直角を向いていて」「長さが同じ」のベクトルを 3 本選ぶことにしましょう。

長さが 1 で、互いに垂直な 3 ベクトルで構成された座標系$\{O:\vec{a},\vec{b},\vec{c}\}$のことを直交座標系と呼びます。

空間座標の世界では、分かりやすさや使いやすさから、もっぱら直交座標系がガンガン使われています。

考えてみれば、高校までの xyz 座標空間も、x 軸・y 軸・z 軸は互いに直交していましたし、長さの単位は x,y,z に関係なく同じでした。

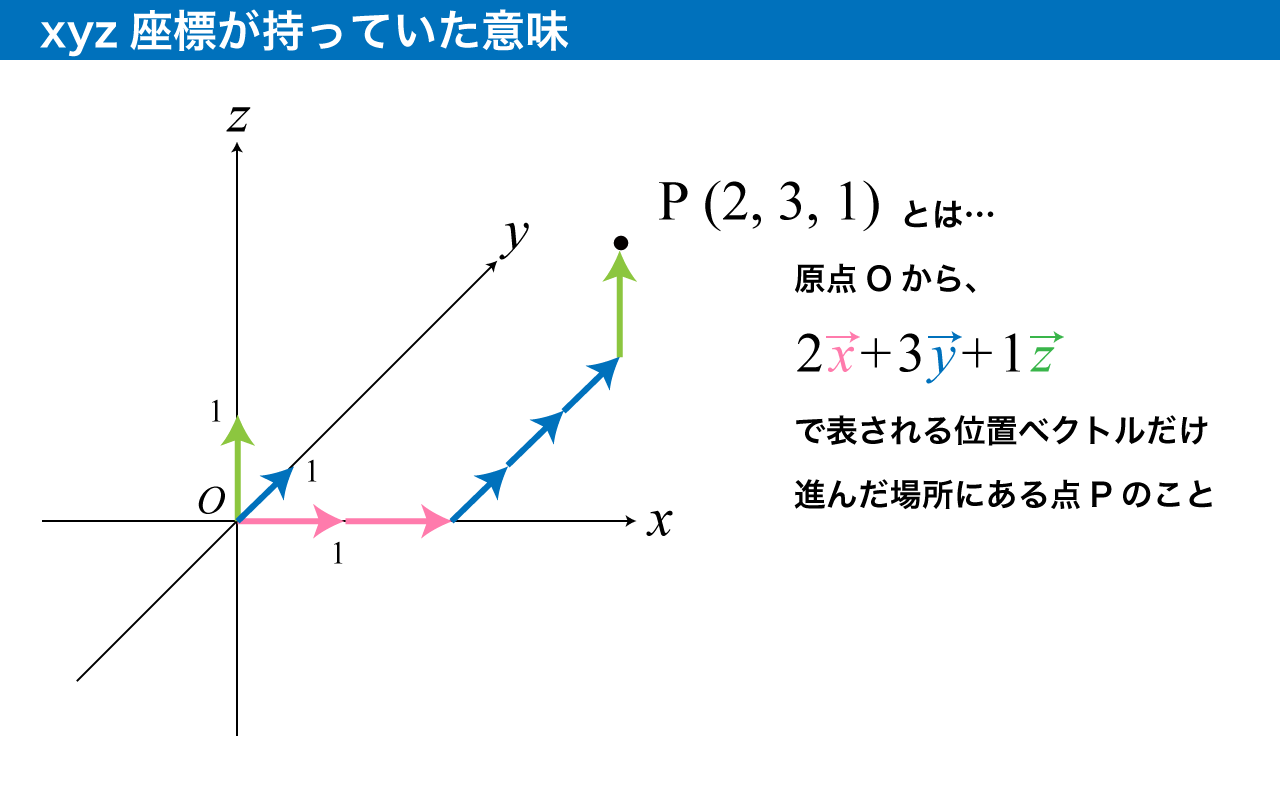
今まで習ってきた「座標」の概念は、こうした形でベクトルと結びついてきたんだなと分かってもらえると今回の記事の目標は達成です！

おわりに

今回は、3 次元空間上の点の位置をベクトルを使って表現することを目指し、そこから「座標系」とはなんたるやについて解説していきました。

このように、ベクトルは空間座標に絡めても利用することができるので本当に汎用性が高いですよね。

次回の記事では、ベクトルを使って直線や平面などを表現したり、面積や体積を求めたりします！

ベクトルで色々な図形を表現する！＞＞