【ベクトル編】内積と外積を画像付きで徹底解説！

2018年4月15日作成2018年7月8日更新

こんにちは、おぐえもん(@oguemon_com)です。

前回の記事では、ベクトルについて、高校で習ったような空間上における定義とその計算方法について扱いました。

今回は、ベクトルの「内積」を復習し、大学で新しく登場する「外積」というものについても触れていきたいと思います。

ベクトルの内積

内積の定義

内積は高校で習いましたよね？

2 つのベクトル $\boldsymbol{a}$ と $\boldsymbol{b}$ について、2 つの始点をくっつけた時にできる角度（ $\boldsymbol{a}$ , $\boldsymbol{b}$ のなす角と言います）を $\theta$ とした時に、「 $|\boldsymbol{a}||\boldsymbol{b}|\cos\theta$ 」で表される値（スカラー）のことを言います。内積は、「 $(\boldsymbol{a},\boldsymbol{b})$ 」や「 $\boldsymbol{a} \cdot \boldsymbol{b}$ 」という風に表します（大学では前者で記すことが多い？）。

ベクトルの内積

$(\boldsymbol{a},\boldsymbol{b})=|\boldsymbol{a}||\boldsymbol{b}|\cos\theta$

簡単に言えば、「2 つのベクトルの大きさの掛け算」×「2 つのベクトルのなす角の cos」ですね！

零ベクトルを含む内積

零ベクトルには向きがないので、「なす角」を考えることができません。そこで、零ベクトルを含む内積を考えるときは、零ベクトルの大きさが「0」であることに着目して、その結果が必ず 0 になるように定めます。

$(\boldsymbol{a},\boldsymbol{o})=(\boldsymbol{o},\boldsymbol{a})=(\boldsymbol{o},\boldsymbol{o})=0$

同じベクトルの内積

同じベクトルは、当然ながら向きが揃っているので、なす角が「0」となります。 $\cos 0=1$ ですので、同じベクトルで内積をとると、

$(\boldsymbol{a},\boldsymbol{a})=|\boldsymbol{a}||\boldsymbol{a}|\cos0=|\boldsymbol{a}|^2$

となります。大きさの 2 乗になるわけですね。つまり、 $\boldsymbol{a}$ が零ベクトルの時を除いて、必ず正の値を取るということです。

内積の性質

内積には次のような性質があります。

$(\boldsymbol{a},\boldsymbol{b})=(\boldsymbol{b},\boldsymbol{a})$

内積は、掛け合わせる順序が結果に影響を与えることはありません。だって、順序を入れ替えたところで、なす角の大きさも、両者の大きさも変わらないので、掛け算の結果は同じになりますからね。

$(\boldsymbol{a},\boldsymbol{b}+\boldsymbol{c})=(\boldsymbol{a},\boldsymbol{b})+(\boldsymbol{a},\boldsymbol{c})$

内積にも分配法則のような性質があります。この性質、成り立つ理由を正しく説明するのは案外難しいですので、頭の体操として考えてみてください。

$(\lambda\boldsymbol{a},\boldsymbol{b})=\lambda(\boldsymbol{a},\boldsymbol{b})$

ベクトルをスカラー倍したもので内積を取ろうが、内積を取ってからスカラー倍しようが結果は変わりません。

$\boldsymbol{a}$ と $\boldsymbol{b}$ が共に零ベクトルでない時、

$(\boldsymbol{a},\boldsymbol{b})=0 \Longleftrightarrow \boldsymbol{a}$ と $\boldsymbol{b}$ は直交している。

零ベクトルでないもの同士の内積を取って、その値が 0 であることと、両者が直角に交わっていることは同値なのです。だって、なす角が 90 度ならば、 $\cos 90=0$ であることから、ベクトルの大きさが 0 でない限り内積 0 と同値ですよね。

ベクトルの外積

内積があれば外積もあります。これは、大学に入って初めて登場する概念です。

外積の定義

外積は内積よりも少し複雑です。簡単にいうならばこんな感じ。

外積とは

2 つのベクトル $\boldsymbol{a}$ と $\boldsymbol{b}$ は、0 より大きな長さをもち、かつ、同じ向きでも逆向きでもありません（つまりなす角が 0 度でも 180 度でもない）。

その時、これらの外積を「 $\boldsymbol{a} \times \boldsymbol{b}$ 」という風に記します。

外積は、内積と異なり「大きさ」と「向き」を持つベクトルであり、次のように定義されます。

大きさ
- ベクトル $\boldsymbol{a}$ と $\boldsymbol{b}$ を隣り合う 2 辺とする平行四辺形の面積とします。
向き
- ベクトル $\boldsymbol{a}$ を、なす角の方向にクリッと回転させて、ベクトル $\boldsymbol{b}$ に重ねる時、それを右ねじに見立てた時にネジが進む方向です。

言葉だけじゃよくわからないと思うんで、図を用意しました！

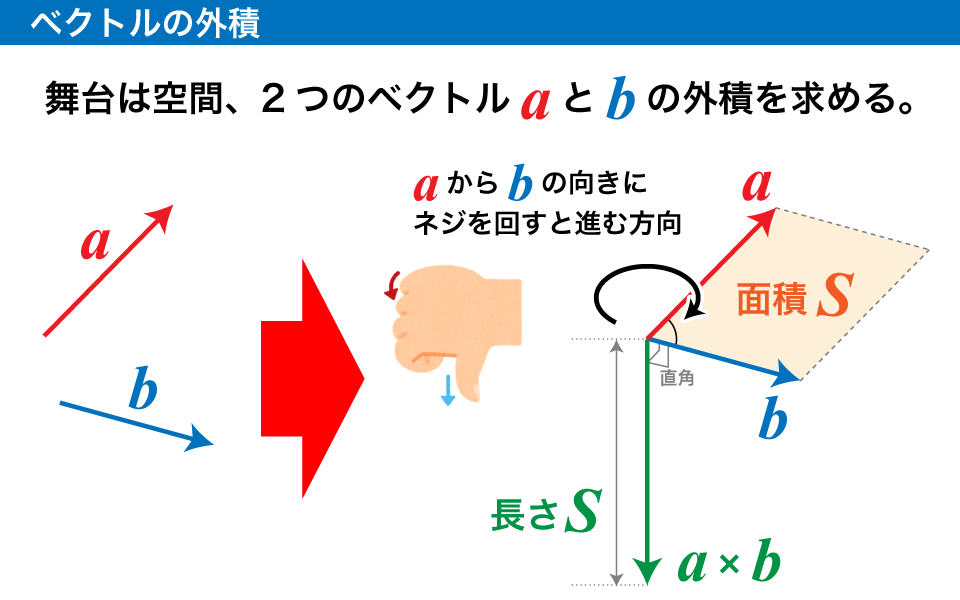
何度も言いますが、外積は、内積と違って「向き」の情報も含む「ベクトル」です！初めて学習する時に忘れがちなので注意してください。

外積の「向き」について、改めて説明します。外積の向きは、「右ねじの法則」みたいな感じで決まります。一般的なネジって、時計回りに回転させると、穴にめり込んでいきます（ネジの先端に向かって進みます）よね？外積もこれと同じで、「×」の左にあるベクトルから右にあるベクトルに向かって回す時に、ネジの先端が進む向きを外積の向きとします。

同方向（または逆方向）を向く2ベクトルの外積

同じ方向を向く 2 つのベクトルの組み合わせだと、平行四辺形が出来上がりません（つまり面積がゼロ）。よって、このような組み合わせで外積を取ると、大きさがゼロの「零ベクトル」となります。

逆方向を向く 2 つのベクトルについても、平行四辺形が出来上がらないので、外積は零ベクトルです。

零ベクトルが含まれる外積

当たり前な話、外積は零ベクトルです。（平行四辺形が出来上がらない）

外積の性質

外積が持つ性質もざっと挙げます。

$\boldsymbol{a} \times \boldsymbol{b}=-\boldsymbol{b} \times \boldsymbol{a}$

順序を入れ替えると、外積の向きが逆になります。これは、右ねじの向きで外積の方向が決まる中で、「回転の向き」が逆転するからですね。

$(\lambda\boldsymbol{a}) \times \boldsymbol{b}=\boldsymbol{a} \times (\lambda\boldsymbol{b})=\lambda\boldsymbol{a} \times \boldsymbol{b}$

スカラー倍は、外積に対して行っても、外積の計算前にどちらかのベクトルに対して行っても結果は変わりません。（どちらかのベクトルをスカラー倍したら、結局平行四辺形の面積がスカラー倍になりますからね）

$\boldsymbol{a} \times (\boldsymbol{b}+\boldsymbol{c})=\boldsymbol{a} \times \boldsymbol{b}+\boldsymbol{a} \times \boldsymbol{c}$

外積でも分配法則が成り立ちます。これの理由を説明するのは内積と同じく割と手間がかかるので、初学者向けの本連載においては割愛します。

最後に

今回は、高校で習った内積を復習するとともに、新しく登場した「外積」というものについても扱いました。外積は、数学だけでなく力学などの物理分野でも登場しますので、理系の方はしっかり理解しておいてくださいね〜

次回の記事では、高校時代に苦手意識を持った方も多い（はずの）「位置ベクトル」について扱います。

3 次元空間と位置ベクトルと座標系を解説！＞＞