線形空間(ベクトル空間)を画像と具体例で解説

2019年9月17日

こんにちは、おぐえもん(@oguemon_com)です。

今回から数回にわたって、「線形空間（ベクトル空間）」に関する解説をします。

線形空間って聞くと難しそうなイメージを受けますが、実際そんなに複雑で難解な話ではありません。頑張って勉強していきましょ〜！

線形空間(ベクトル空間)って何？

簡単に言えば、今まで習ったベクトルと同じような性質を持つある要素の集合のことです。

ベクトルの演算にはいくつかの基本的な性質がありましたよね？

注意すべき行列の性質

おぐえもん.com

この性質って何もベクトルだけが持っているものではありません。そこで、ベクトルと同じような性質を持つ色んなものを「線形空間」（ベクトル空間とも言います）というカテゴリに入れて、これらの性質をまとめて考えようとするのがこの単元のコンセプトです。

線形空間の条件

1.集合である

まず、線形空間というのは 集合(あるものの集まり) のことを言います。集合の中でも、一定の条件を満たせば線形空間と言えるわけです。集合は有限でも無限でも構いません。「整数」みたいな無限個ある集合でも条件さえ満たせば OK です。

ここでは、ある集合を $V$ という記号で表して考えていきます。

2.「和」と「スカラー倍」の演算ルールがある

さて、ある集合 $V$ が線形空間なのかどうかを考える上で、2 つの演算ルールが用意されていることが前提になります。それが「和」と「スカラー倍」です。どっちも馴染みのある言葉ですね。

和とスカラー倍

和

$V$ の中にある任意の2つの要素 $\boldsymbol{a}$ と $\boldsymbol{b}$ を与えると、「 $\boldsymbol{a}+\boldsymbol{b}$ 」と表すことができる $V$ の中の要素を定められる演算です。

（例えば、自然数の和は、自然数 2 つを与えて足し合わせることで自然数に含まれる 1 つの値を定めることができます。）

スカラー倍

$V$ の中の要素 $\boldsymbol{a}$
実数集合または複素数集合の中にある値 $\lambda$ （スカラー）

の 2 つを与えると、「 $\lambda\boldsymbol{a}$ 」と表すことができる $V$ の中の要素を定められる演算です。

ポイントは、 $V$ の中の要素で定められることです。 $V$ の要素を与えて、 $V$ の中にない何かが定められたらダメなんですね。例えば、整数の集合に対する演算のルールで、整数を与えたのに小数とかが返ってくるのは NG なのです。

3.「和」と「スカラー倍」が計7つの条件を満たす

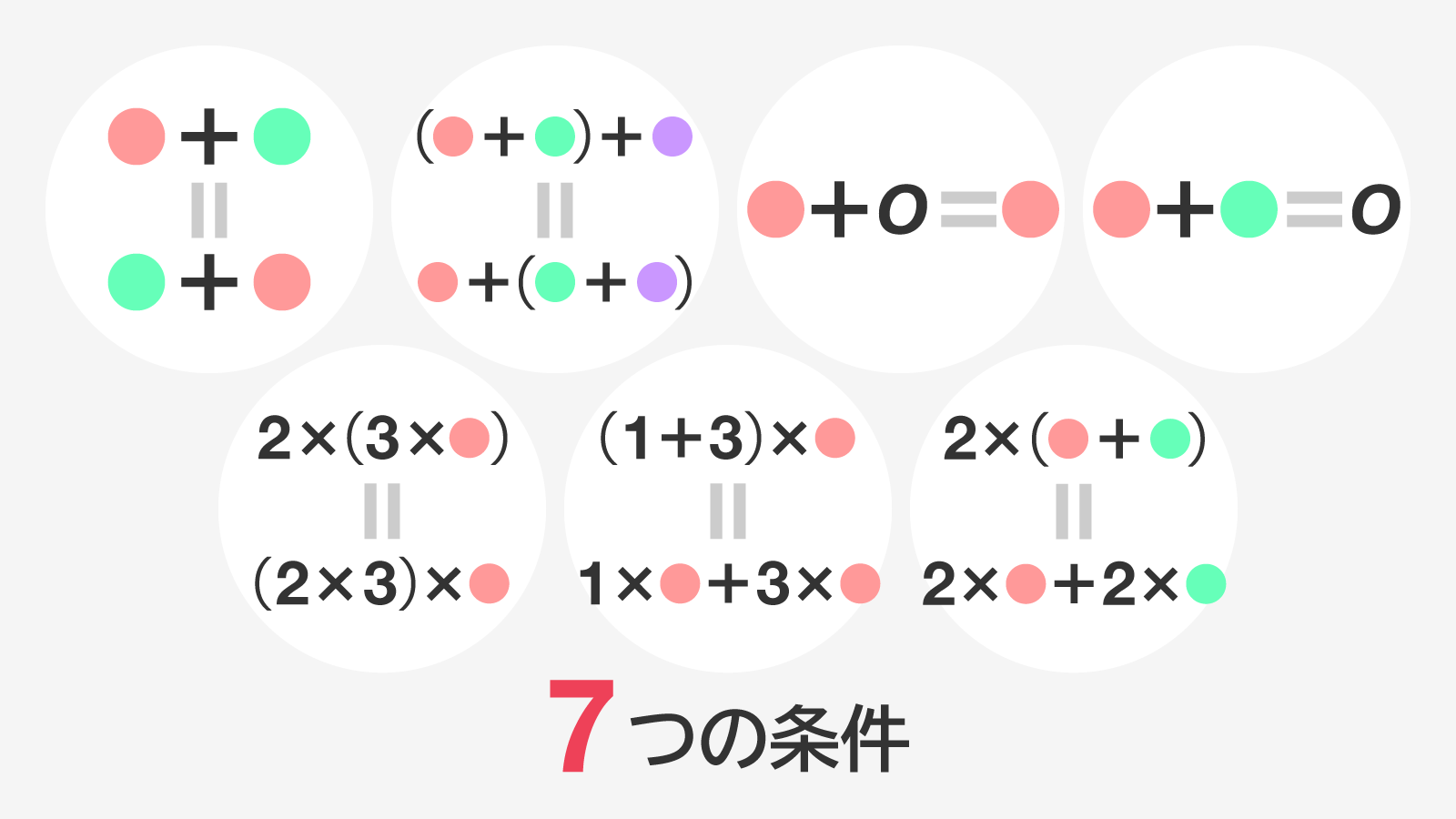
集合 $V$ に対して「和」と「スカラー倍」の演習ルールが用意されているのに加えて、演算ルールがある条件を満たしていなければなりません。

「和」が満たすべき条件

（入れ替え可能）任意の $\boldsymbol{a},\boldsymbol{b}$ について次の式が成立。 $\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{a}$
（計算順序不問）任意の $\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$ について次の式が成立。 $(\boldsymbol{a}+\boldsymbol{b})+\boldsymbol{c}=\boldsymbol{a}+(\boldsymbol{b}+\boldsymbol{c})$
（零-ゼロの存在）任意の $\boldsymbol{a}$ について次の式を成立させる $\boldsymbol{o}$ が存在。 $\boldsymbol{a}+\boldsymbol{o}=\boldsymbol{a}$
（逆元-マイナスの存在）任意の $\boldsymbol{a}$ と上述の $\boldsymbol{o}$ について、次の式を成立させる $\boldsymbol{x}$ が存在。 $\boldsymbol{a}+\boldsymbol{x}=\boldsymbol{o}$

「和」というのは、2 つの要素に対して定義されるものです。しかし、性質 1 と 2 が成り立ってくれるおかげで、3 つ以上の要素の和を「b+a+c」みたいな感じで並び方や計算順序を気にせず記述できるわけです。

そして、性質 3 と 4 が成り立ってくれるおかげで、「和」の定義だけで、私たちが「引き算」と呼んでいる演算を行うことができます。引き算は、性質 3 に由来する「マイナスの数」の和です。

「スカラー倍」が満たすべき条件

$\lambda$ と $\mu$ はスカラーです。そして、任意の $\boldsymbol{a}$ について、 $1\boldsymbol{a}=\boldsymbol{a}$ です。

（計算順序不問）次式が成立。 $\lambda(\mu\boldsymbol{a}) = (\lambda\mu)\boldsymbol{a}$
（スカラーの分配）次式が成立。 $(\lambda+\mu)\boldsymbol{a} = \lambda\boldsymbol{a} + \mu\boldsymbol{a}$
（要素の分配）次式が成立。 $\lambda(\boldsymbol{a} + \boldsymbol{b}) = \lambda\boldsymbol{a} + \lambda\boldsymbol{b}$

さて、これら 7 つの条件って、ベクトルの「和」と「スカラー倍」の演算が持っている性質そのものなんですよね。今まで扱ってきたような「数字の並び」としてのベクトル以外にも、このような性質を持つ集合は色々あります。そんな集合を線形空間（＝ベクトル空間）と呼び、集合の中にある要素をベクトルと呼びます。

高校までは、「向きと大きさ」を表す存在だったベクトルは、線形代数の序盤で「ひと並びの数字列」にまで意味が広がり、ついには、「和とスカラー倍があって一定の条件を満たす集合の要素」として究極に抽象化されちゃいました。

実線形空間と複素線形空間

線形空間は、スカラー倍の演算に用いるスカラーの値の集合によってその呼び名を細かく分類できます。

まず、スカラーとして実数を使用することが前提の場合、線形空間の中でも実線形空間(実ベクトル空間)または、実数上の線形空間(ベクトル空間)と言います。

一方で、スカラーとして複素数を使用することが前提の場合、複素線形空間(複素ベクトル空間)または、複素数上の線形空間(ベクトル空間)と言います。

線形空間の例

線形空間として挙げられるものは、何も数字の並びとしてのベクトルの集合だけではありません。ここでは、線形空間と言える集合の中でも主なものを集めました。

平面ベクトル＆空間ベクトル

平面ベクトル全体の集合や、空間ベクトル全体の集合は、線形空間としての条件を満たすので、線形空間の 1 つです。(高校から習ってきた元祖ベクトルみたいな存在ですので当然感がありますけど笑)

【ベクトル編】高校のベクトルを基礎から復習！＋α

おぐえもん.com

n個の実数の組

n 個の実数の組 $(a_1,a_2,...,a_n)$ 全体の集合を $\boldsymbol{R}^n$ とし、集合 $\boldsymbol{R}^n$ に対して和と実数倍(スカラー倍)と次のように定めます。

和： $(a_1,...,a_n) + (b_1,...,b_n) = (a_1+b_1,...,a_n+b_n)$

実数倍： $\lambda(a_1,...,a_n) = (\lambda a_1,...,\lambda a_n)$

※ただし $(a_1,...,a_n) = (b_1,...,b_n) \Leftrightarrow a_1=b_1,...,a_n=b_n$

この時、 $\boldsymbol{R}^n$ は実数上の線形空間です。これは、線形代数の序盤からお世話になっている 「数字の並びとしてのベクトル」が実線形空間 ってことを表しています。

ちなみに、実数を複素数に置き換えると、それは複素線形空間として成立します。

行列

実数を成分とする $n$ 行 $m$ 列行列の全体の集合は実数上の線形空間です。

多項式

実数を係数とする $x$ についての $n$ 次以下の多項式

a_0x^n+a_1x^{n-1}+...+a_n

の全体の集合は、従来の和と実数倍(スカラー倍)について、上述の条件を満たします。つまり、実数上の線形空間です。

これが一番意外なんじゃないでしょうか。多項式なんて今までの考え方ではベクトルの「べ」の字もありませんでしたが、線形空間内の 1 ベクトルとして扱うことができます。

おわりに

今回は、今までのベクトルの概念をより広いものに対して当てはめる「線形空間」というものの定義について触れました。次からは、線形空間の世界における「1 次独立」や「次元」などのお話を進めていきます。(正直今まで習ってきたベクトルの話とあまり変わりません笑)

【線形空間編】基底と次元と成分

おぐえもん.com