【ベクトル編】ベクトルで色々な図形を表現する
大学1年生もバッチリ分かる線形代数入門

【ベクトル編】ベクトルで色々な図形を表現する

こんにちは、おぐえもん(@oguemon_com)です。

前回の記事では、「座標 × ベクトル」をテーマに掲げ、馴染み深い 3 次元座標をベクトルを使って作る方法について解説しました。

今回は、ベクトルを使って、直線や平面、そしてベクトルが作る図形の面積や体積を表現する方法について解説します。

直線を表現する

ベクトルを使って直線を表現してみましょう。

方向ベクトル

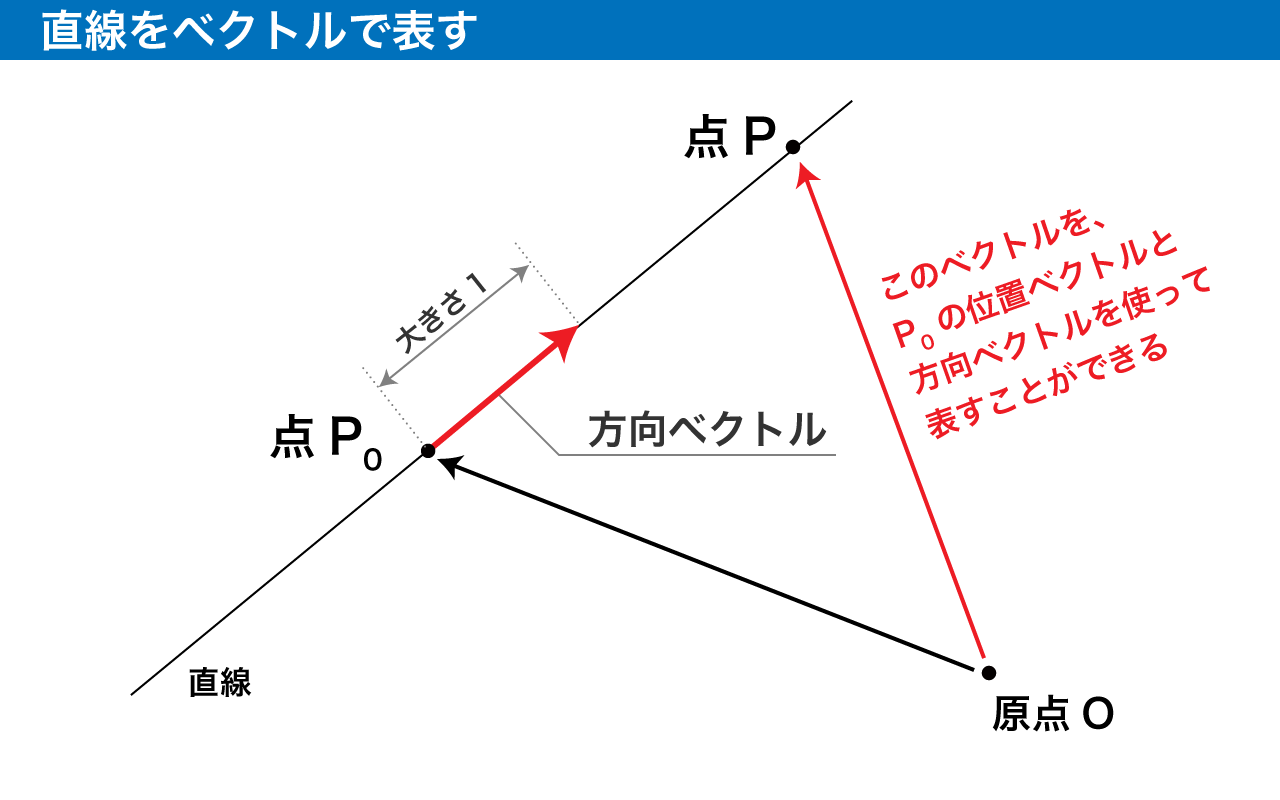
直線は、まっすぐに伸びる線のことです。つまり、直線と同じ向きを持つベクトルを用意すると、そのベクトルを実数倍することで直線上の点を表現することに一役買いそうです。

このように、直線の方向を示す（つまり直線と平行な）ベクトルの中でも、特に長さが 1 の単位ベクトルのことを方向ベクトルと言います。

ベクトル方程式

方向ベクトルだけでは、直線の向きこそ分かりますが、直線がどこにあるのか分かりません。そこで、直線上の点を基点として適当に選んで、その位置ベクトルを用いることにします。

つまり、直線をベクトルで表すためには、「直線と同じ向きのベクトル」「直線上の適当な点の位置ベクトル」の 2 つを用意する必要があります。

ある直線は方向ベクトルl\boldsymbol{l}をもつとします。直線上の適当な点P0P_0を基点とし、直線上の任意の点PPを表現する方法を考えます。

この時、OP⃗=x,OP0⃗=x0\vec{OP}=\boldsymbol{x}, \vec{OP_0}=\boldsymbol{x_0}と置くと、

x=x0+tl\boldsymbol{x} = \boldsymbol{x_0} + t\boldsymbol{l}

と表現できます。ただし、ttは適当な実数です。

このように、ベクトルを使うと、直線を上のような等式で表現することができます。これを直線のベクトル方程式と呼びます。

平面を表現する

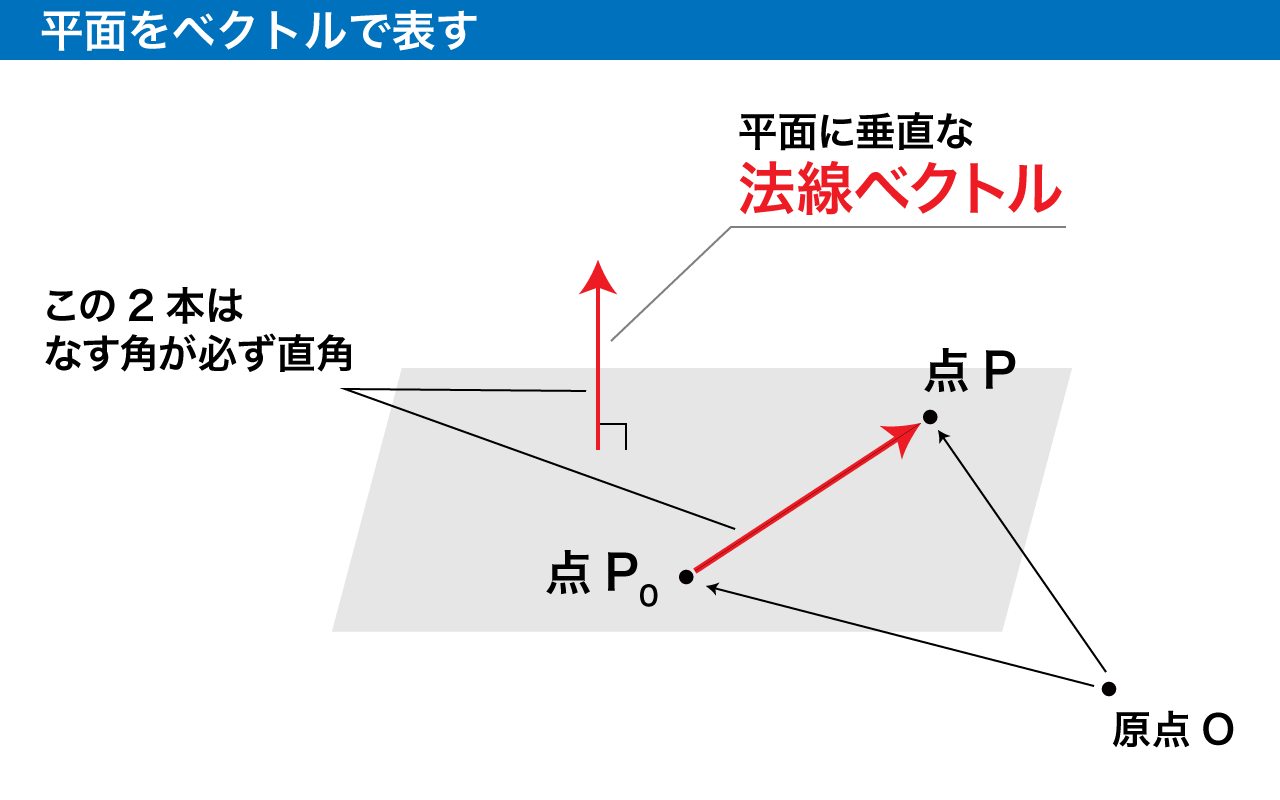
平面についても、「基点となる平面上の点」と「平面の向きを象徴するベクトル」の 2 つを用意してベクトル方程式を作ります。

平面の向きを象徴するベクトルとは何でしょう？平面は直線と違って、広がりがあるので「向き」と言われても困りますよね。

実は、「平面に垂直な方向」のベクトルを用意することで、平面の広がりを遠回しに、だけど簡単に表現することができます。このような平面に垂直なベクトルを法線ベクトルと言います。

平面の方程式は、平面上のベクトルと、法線ベクトルがいかなる場合も垂直であることを利用します。

直線と同じように、平面上の適当な点P0P_0を基点とし、平面上の任意の点PPを表現する方法を考えます。ある直線は法線ベクトルn\boldsymbol{n}をもつとします。

この時、OP⃗=p,OP0⃗=p0\vec{OP}=\boldsymbol{p}, \vec{OP_0}=\boldsymbol{p_0}と置くと、

(p−p0,n)=0(\boldsymbol{p} - \boldsymbol{p_0}, \boldsymbol{n}) = 0

と表現できます。

つまり、平面上の 2 点を結ぶベクトルは平面上にありますが、それは法線と垂直なので両者の内積が 0 になるだろって理屈で方程式を組み立てるのです。

面積を表現する

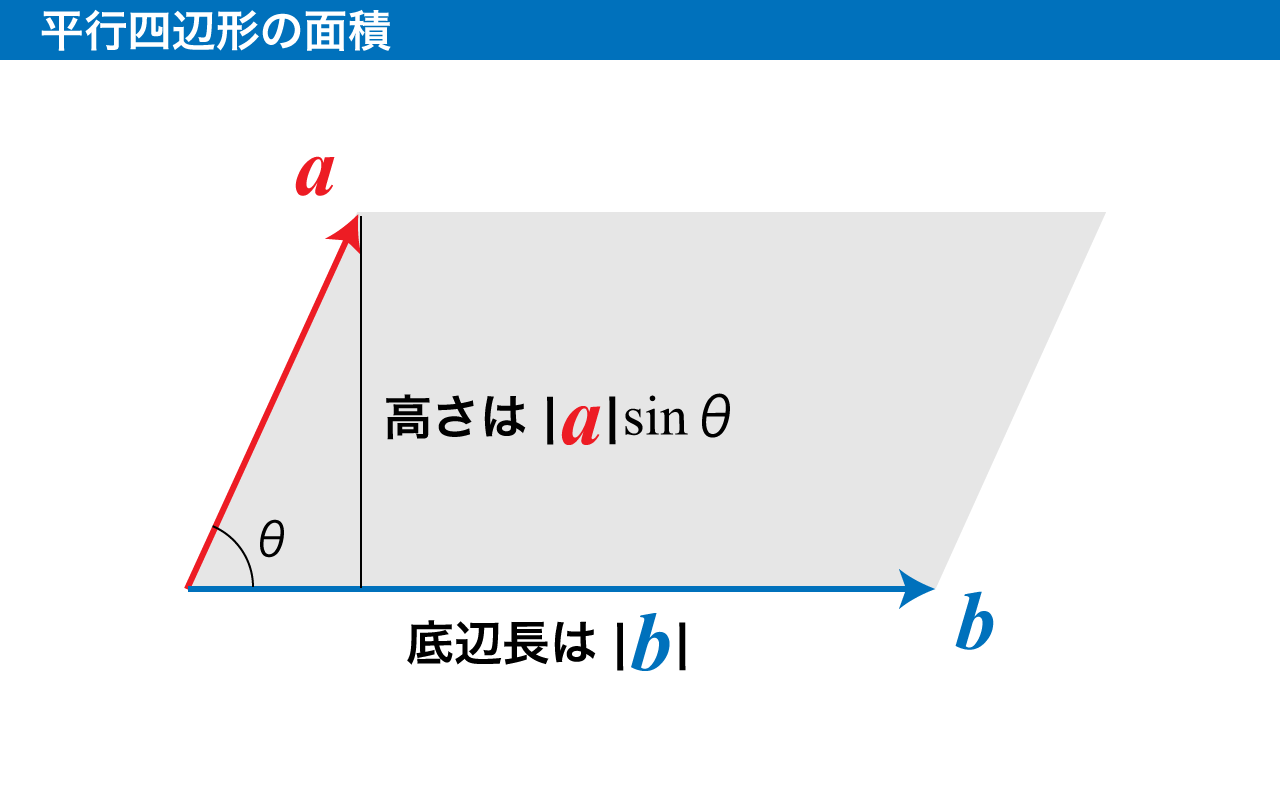
ベクトルa⃗\vec{a}とb⃗\vec{b}が織りなす平行四辺形の面積SSの表現方法を考えましょう。

まず、次のように表現できますよね？

S=∣a⃗×b⃗∣S=|\vec{a} \times \vec{b}|

つまり 2 つのベクトルの外積の長さです。これは当たり前ですよね？笑

だって、外積の長さって平行四辺形の面積だと定義されているのですから。

他の方法も考えましょう。

平行四辺形の底辺をb⃗\vec{b}とすると、平行四辺形の高さは、a⃗\vec{a}の長さにsin⁡θ\sin\thetaを掛けたものになります（θ\thetaはなす角）。

ですので、「S=∣b⃗∣∣a⃗∣sin⁡θS = |\vec{b}||\vec{a}|\sin\theta」となります。

ところで、sin⁡θ\sin\thetaはここでは絶対に 0 以上の値を取るので、sin⁡θ=1−cos⁡2θ\sin\theta = \sqrt{1 - \cos^2\theta}としても問題ありません。

ですので、

S=∣b⃗∣∣a⃗∣sin⁡θ=∣b⃗∣∣a⃗∣1−cos⁡2θ=∣a⃗∣2∣b⃗∣2−∣a⃗∣2∣b⃗∣2cos⁡2θ=∣a⃗∣2∣b⃗∣2−(a⃗,b⃗)2\begin{aligned} S &= |\vec{b}||\vec{a}|\sin\theta \\ &= |\vec{b}||\vec{a}|\sqrt{1 - \cos^2\theta}\\ &= \sqrt{|\vec{a}|^2|\vec{b}|^2 - |\vec{a}|^2|\vec{b}|^2\cos^2\theta}\\ &= \sqrt{|\vec{a}|^2|\vec{b}|^2 - (\vec{a},\vec{b})^2} \end{aligned}

となります。

体積を表現する

隣り合うベクトルa⃗\vec{a}、b⃗\vec{b}、c⃗\vec{c}が織りなす平行六面体の体積VVを求めましょう！

まず、a⃗\vec{a}、b⃗\vec{b}が織りなす平行四辺形を六面体の底面とします。

そして、a⃗\vec{a}、b⃗\vec{b}の外積a⃗×b⃗\vec{a} \times \vec{b}とc⃗\vec{c}のなす角をθ\thetaとすると、高さは「∣c⃗∣cos⁡θ|\vec{c}|\cos\theta」と表現できます。

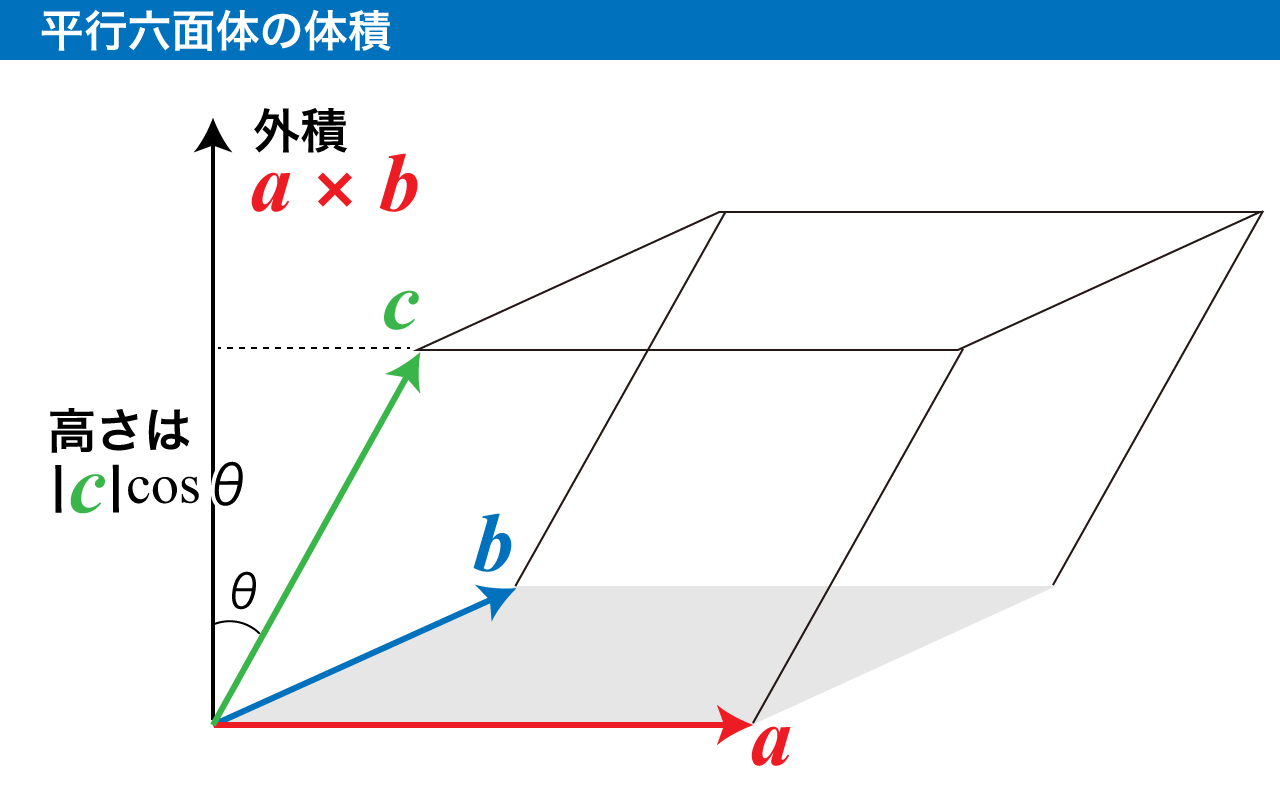
よって、

V=∣a⃗×b⃗∣∣c⃗∣cos⁡θV=|\vec{a} \times \vec{b}||\vec{c}|\cos\theta

となります。外積の長さが登場したのは、底面の面積を表しているからですよ。

上の式は、つまり外積a⃗×b⃗\vec{a} \times \vec{b}とc⃗\vec{c}の内積そのものですよね？

ですので次のように変形できます。

V=(a⃗×b⃗,c⃗)V=(\vec{a} \times \vec{b}, \vec{c})

ここで、上の式の右辺をスカラー 3 重積といい、まとめて (a⃗,b⃗,c⃗)(\vec{a}, \vec{b}, \vec{c})のように記述します。

スカラー3重積

(a⃗,b⃗,c⃗)=(a⃗×b⃗,c⃗)(\vec{a}, \vec{b}, \vec{c}) = (\vec{a} \times \vec{b}, \vec{c})

ちなみに、a⃗={a1,a2,a3},b⃗={b1,b2,b3},c⃗={c1,c2,c3}\vec{a}=\{a_1, a_2, a_3\}, \vec{b}=\{b_1, b_2, b_3\}, \vec{c}=\{c_1, c_2, c_3\}と成分表示すると、六面体の体積、すなわち(a⃗,b⃗,c⃗)(\vec{a}, \vec{b}, \vec{c})の値は、

(a⃗,b⃗,c⃗)=∣∣a1a2a3b1b2b3c1c2c3∣∣(\vec{a}, \vec{b}, \vec{c}) = | \left| \begin{array}{ccc} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right| |

となることが知られています（右辺は行列式の絶対値）。証明は決して難しくないので挑戦してみよう！

おわりに

今回は、ベクトルを使って色々な図形を表現したり、面積や体積を求めてみました。

次回の記事では、ベクトルの内積と外積を成分を用いて導く方法について扱います！

ベクトルの成分で内積と外積を求める！＞＞

▲ トップへ戻る