【発売中】おぐえもんの線形代数入門サイトが書籍化！絶対買うべき3つの理由
大学1年生もバッチリ分かる線形代数入門

【発売中】おぐえもんの線形代数入門サイトが書籍化！絶対買うべき3つの理由

500 万以上のアクセスを誇る、おぐえもん.com の名物コンテンツ「大学 1 年生もバッチリ分かる線形代数入門」が書籍化しました！

現在、Amazon をはじめ各書店にて好評販売中です！書店は大規模店舗に限られるので、Amazon がオススメです。

買いたくない人は、大学図書館を使うのも手です。京都大学をはじめ 40 以上の大学図書館に本書が並んでいます！（このサイトに並ぶ大学と慶應大学）

大学数学を勉強するとき、教科書を読んでいて、

やたらと説明が難解だし、見にくいデザインだな…

と思った人は多いでしょう。

「大学 1 年生もバッチリ分かる線形代数入門」は、そうした現状を踏まえて、「やさしい・見やすい・読みやすい」をモットーに、線形代数のさわりを簡単に理解できる本に仕上げました！

教科書選びに悩んでいる方、大学の講義で指定されている教科書が難解で入門書を探している方にピッタリの本ですので、最後まで読んでどんな本か知っていただきたいです！！

本書を選ぶ3つの理由

従来の教科書の多くには、次のデメリットがありました。

  • 難しい。著者の多くは数学者で、厳密な議論や隅々の証明に重きをおきがちだからです。
  • 見にくい。昭和時代の本が未だ現役なのと、数式が盛り込まれた本は、デザインにコストがかかるからです。
  • 読みにくい。文字数を減らすために、大切な部分を簡素な説明に留められていることが多々あります。

読者に教える気があんのかって感じですよね。

そこで、「大学 1 年生もバッチリ分かる線形代数入門」は、こうした従来の教科書の課題にアプローチすることを目指して執筆しました。

本書は、次の 3 つのポイントを押さえてます。

POINT1：やさしい

初学者にとってまず必要なのは、個々の厳密な理論を知ることでなく、線形代数の大まかな流れをザックリ理解することです。

本書の内容は、厳密さよりもやさしさを優先しました。

POINT2：見やすい

難解な理論もデザインの力で分かりやすくなります。本書は、分かりにくい箇所に直感的な図解を加えたり、各単元の意図が明確になるレイアウトを採り入れるなど、見やすさにこだわりました。

POINT3：読みやすい

従来の大学数学の入門書が難しい理由のひとつに難解な文章構成と言い回しが挙げられます。本書は、文章構成を明快にして、誰でも分かる簡単な言い回しを徹底しました。

購入いただいた方から、早速わかりやすいコメントをいただきました！！こうしたポイントが読者の方にも伝わっていて嬉しいです！！

本屋でたまたま見かけて購入しました！
えっと・・・・、学校の指定教科書の10倍わかりやすいっす！頭の中にイメージが入りやすいのが自分が好きなところです。 https://t.co/QkMkRUXJpU — Hiro (@soraki_unicks) July 12, 2021

こんな人にオススメ！

こんな人は、本書がオススメです！

  • 線形代数を独学ではじめたいけど、まず何の本を買おうか迷っている人。
  • 線形代数を履修しているけど、講義も教科書もワケワカメで、補助的な本が欲しい人

一方で、次のような人は他の本が良いかもしれません。

  • すでに線形代数をある程度理解していて、発展的な本を探している人。
  • 厳密な論理のもとで展開される純粋数学として線形代数を勉強したいストロングスタイルの人。

大学1年生で習う範囲をしっかりカバー

本書は、やさしさが特徴ながら、理工系の学生が大学 1 年生で履修する範囲をほとんど押さえています！

そして、多くの講義で採用されている学習の順番に倣って章を並べているので、講義と並行してスムーズに学べます！

ちなみに、236 ページあります。スカスカすぎず、重すぎずのいい感じのボリュームです！

本書の目次

  • 基本編（1年生前期）
    • 線形代数とは何か、行列とは何かからはじまり、行列の基本的な事柄を解説します。
  • 連立方程式編（1年生前期）
    • 中学で学んだ連立方程式の解き方を復習して、解を網羅する方法や、行列との繋がりを解説します。
  • 行列式編（1年生前期）
    • 行列を特徴づける重要な指標「行列式」の一般的な定義や重要な性質、これを用いた逆行列の求め方、連立方程式との関係を解説します。
  • 空間ベクトル編（1年生前期〜後期）
    • 高校の「ベクトル」単元をここで復習して、線形代数で習う「ベクトル」との違いを考えます。
  • 線形空間編（1年生後期）
    • 線形代数の試みの一つである、身の回りの色々なものを連立方程式の要領で考える理論作りを進めます。
  • 固有値編（1年生後期）
    • 行列式と並ぶ、行列の重要な指標に「固有値」「固有ベクトル」があります。両者の特徴と、これを用いた行列の変形方法を解説します。
  • 線形写像編（1年生後期〜2年生）
    • 2つの集合の要素間にある一定の条件を満たす対応を線形写像といいます。この性質を明かして、本書の集大成として線形代数の本質に迫ります。

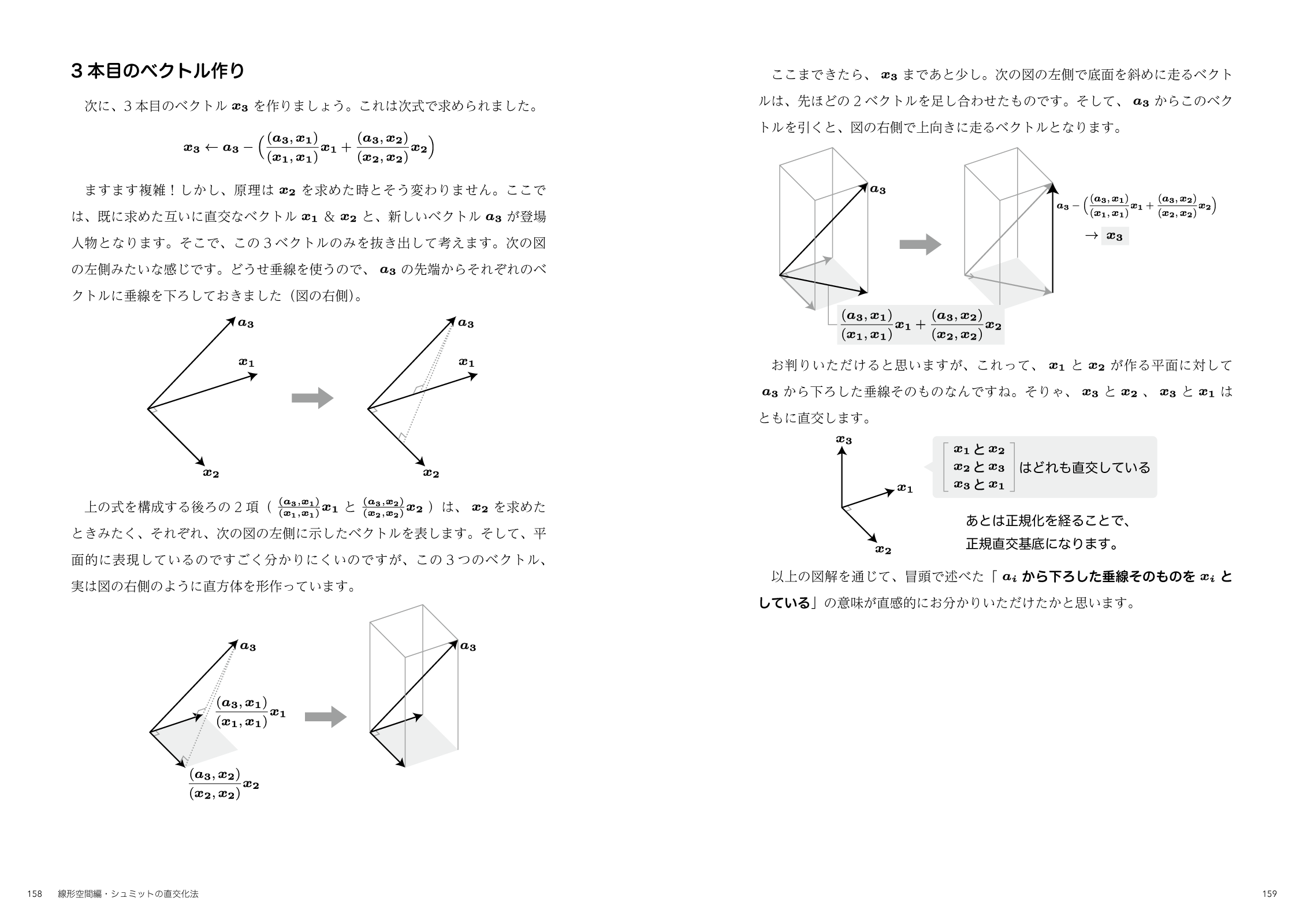
サンプルページ

本の中身をちらっとご紹介。分かりやすさを意識したデザインを採り入れました！

販売ページはこちらから！

現在、Amazon や各書店で販売されております！みんな是非とも買ってください！！

紀伊国屋や丸善など都市部の大型書店だけでなく、大学生協の書店などにもあると思います。店頭で見かけた際は、ぜひとも立ち読みしてみてください！

また、本書は 40 以上の大学図書館（このサイトに並ぶ大学と慶應大学）にもあります。お金がなくて買えない方は、図書館で借りるのもアリです。

「うちの大学図書館にないんだけど」って方は、ぜひとも図書館で配架のリクエストをしてください！！

▲ トップへ戻る