【線形写像編】写像の基礎(像・全単射・写像の合成)
こんにちは、おぐえもん(@oguemon_com)です。
今回から、線形代数の中でも後半に習うことの多い「線形写像」をテーマにして数回の連載を始めます!
線形写像は、線形代数の講義の中でも抽象度が高い単元です。その代わり、線形写像の理論によって、連立方程式や図形ベクトルなど、線形代数で扱ってきた様々なモノをひとまとめにして考えることができます!
初回である今回は、線形写像の定義に先立ち「写像」の基本用語を解説します。
写像と像
2 集合の要素の対応を写像と言います。そして、ある写像によって対応づけられた「先」の要素もしくは集合を像と言います。
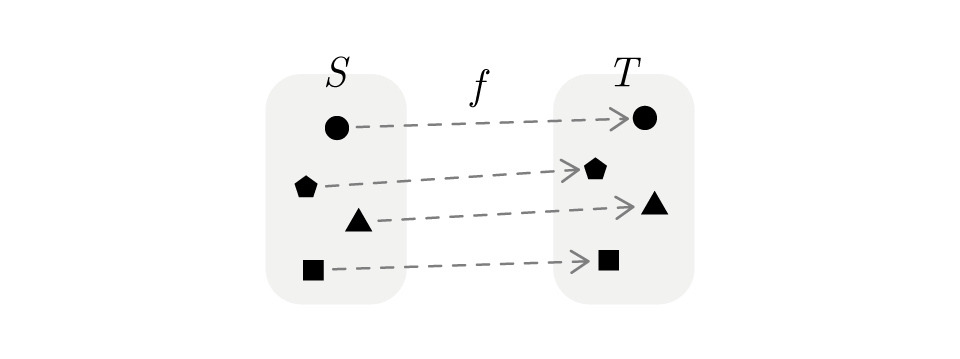
2 つの集合とがある。のどの要素もの何らかの 1 要素に対応しているとき、この対応付けを、集合から集合への写像と言い、やなどの文字を使って次のように書く。
写像によって、集合のある要素に対応づけられた集合の要素を、のによる像と言い、と書く。次のように書くこともある。
集合の全て要素にそれぞれ対応する像をまとめてできる集合を、のによる像と言い、と書く。は、の部分集合である。
と記すなんて、まるで関数みたいですね。実際、高校の数学 II などで扱ってきた関数は、実数集合から実数集合への写像といえます。
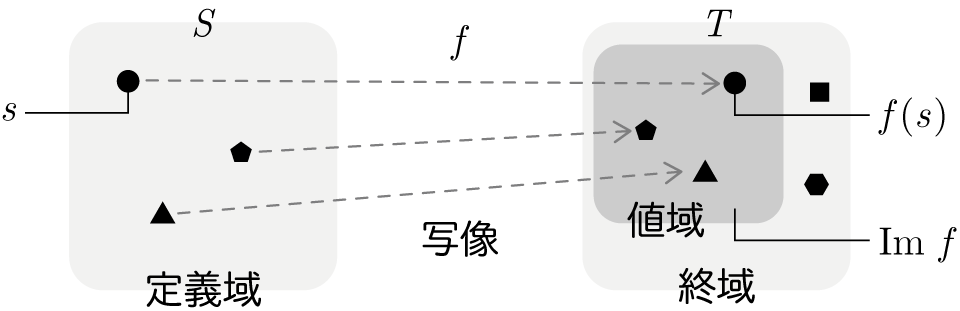
上の画像の通り、対象元の集合や対象先の集合などに応じて、定義域、値域などの用語が与えられています。これもまた関数みたいですね。
写像は、ある要素に対して、像がただ 1 つに決まることが前提です。となるの要素が複数ある場合、は写像ではありません。例えば、と定義されるような対応は写像ではありません。
単射と全射
単射(1対1の写像)
集合の要素が異なれば、対応するの要素も異なる写像を単射または1 対 1 の写像と言います。
下の式を満たす写像を単射または1 対 1 の写像と言う。
上の式は、その対偶をとって「ならば」とすることもあります。
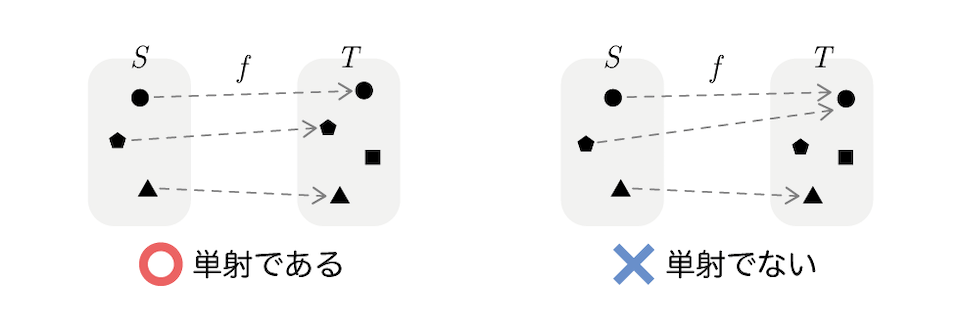
右の例は、の 2 つの要素がの 1 要素(● の要素)に対応しているので、単射ではありません。
全射(上の写像)
集合の要素全ての要素が、集合の何らかの要素と対応する写像を全射または上の写像と言います。
集合の任意の要素に対して、となる集合の要素が存在するとき、写像を全射または上の写像と言う。
全射では、が成り立ちます。
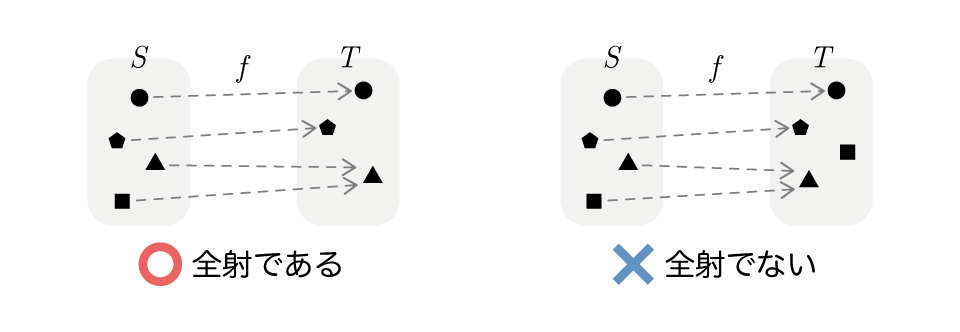
右の例は、の要素の中にの対応先にもなっていないものがある(■ の要素)ので、全射ではありません。
全単射
写像が単射かつ全射のとき、これを全単射と言います。簡単にいうと、両者の集合の要素が漏れなく 1 対 1 に対応する写像です。
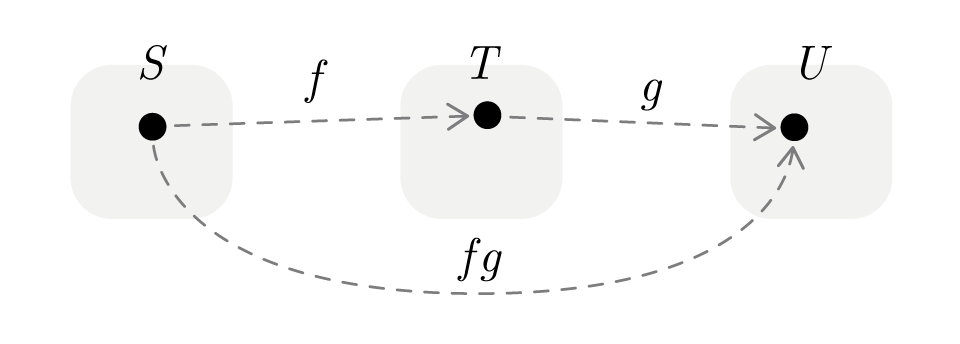
写像の合成
関数に合成関数があったように、写像でも合成を考えることができます。
3 つの集合に対して、写像と写像が定義されているとき、の要素との要素を対応づける写像を、との合成写像といい、と書く。