こんにちは、おぐえもん(@oguemon_com)です。
当サイトにおける線形代数連載も中盤に差し掛かりましたが、みなさん線形代数には慣れてきましたか？
さて、線形代数では「ベクトル」を「数字が縦or横に一直線に並んだもの」として扱っていますが、もともと高校でベクトルを習った時って「平面or空間を走る矢印」でしたよね？
ベクトルは、元々はただの数字の並びです。しかし、平面や空間と絡めると性質を直感的に理解できるということで、高校ではそのように教えているのですよね。
そこで、この記事から数回に亘って、「ベクトル×空間」をテーマに掲げて、高校で習ったことの復習も兼ねながら、ベクトルがもつ幾何学的な意味について改めて解説したいと思います！
ベクトルの基本
ベクトルとは
空間or平面における「ベクトル」とは次のような量を言います。
「向き」と「大きさ」をもつ量のこと。
大きさだけなら「スカラー」と呼ばれます。スカラーに「向き」という新しい情報が加えられることで「ベクトル」となるのです。
ベクトルでは、大きさと向き以外の情報、例えば「位置」などの情報を含みません。そのため、大きさと向きさえ同じならば、矢印がどこから伸びてようが同じベクトルとして扱います。
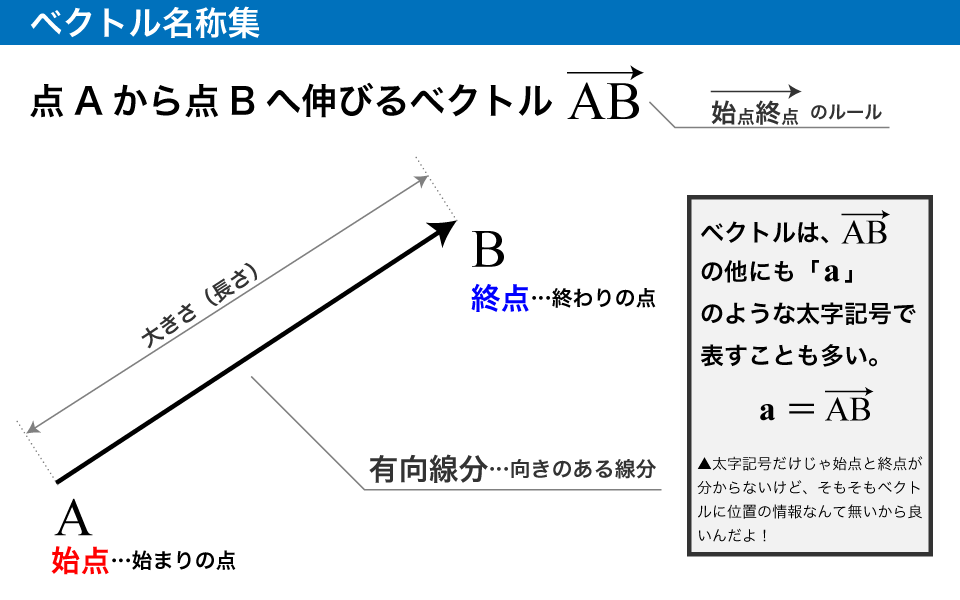
ちなみに、ベクトル\(\boldsymbol{a}\)の大きさ（長さ）は「\(|\boldsymbol{a}|\)」という風に表現します。\(|\boldsymbol{a}|\)はスカラーですので、「1」「4.5」みたいな値を取ります。
零ベクトルと単位ベクトル
大きさが「1」のベクトルを「単位ベクトル」と言います。どの向きを向いていても、大きさが1ならば単位ベクトルです。
そして、大きさが「0」のベクトルを「零ベクトル」と言います。大きさが0ということは、ベクトルの始点と終点が重なっていることを表します。この時、ベクトルにこれといった向きはありません。零ベクトルは、単位ベクトルと違って「向きなし、長さ0」という唯一のベクトルを表すため、これを「\(\boldsymbol{o}\)」という記号で表します。
これらみんな高校で習ったよね？笑
ベクトルの計算
ベクトルの足し算
2つのベクトルを足す方法は、足されるベクトル（＋の前にある方）の終点と、足すベクトル（＋の後ろ）の始点を繋げて、前者の始点から後者の終点へベクトルを伸ばすというやり方です。図にしたら分かりやすいです。
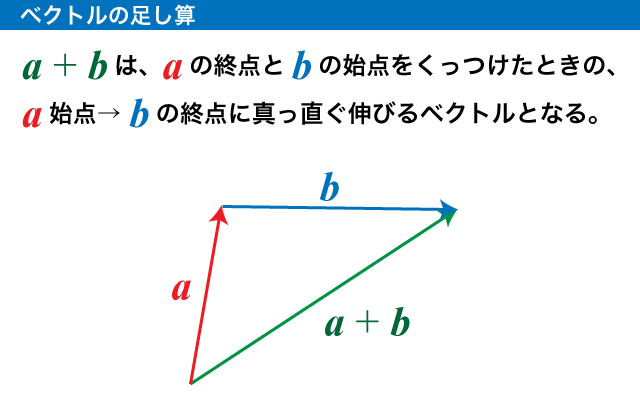
ちなみに、零ベクトルを加えても、結果は変わりません（零ベクトルは始点と終点が同じだから）。
ベクトルの引き算
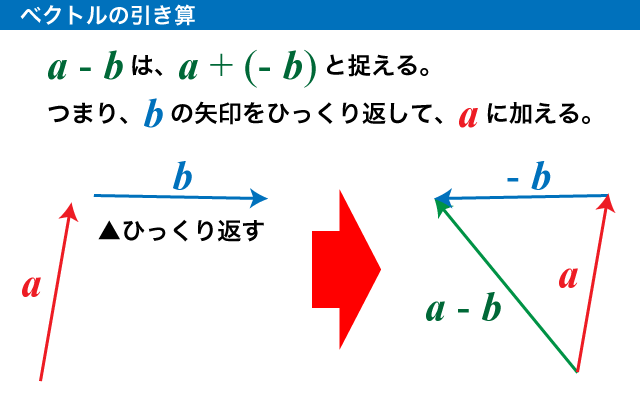
2つのベクトルの引き算は、マイナス付きの足し算と捉えます。
ベクトルを「マイナス」すると、元のベクトルの始点と終点が入れ替わります（矢印の向きが逆になる）。ですので、引くベクトル（-の後ろ）の向きを逆転して、足し算しましょう。
ベクトルのスカラー倍
ベクトルにスカラー （1とか10.5みたいな値）を掛けることができます。そうすると、ベクトルの向きは変わらず、大きさ（長さ）だけが掛け算されます。（ただし大きさがマイナスになったら、向きは反対になります）
長さ5のベクトル\(\boldsymbol{a}\)に10を掛ける。その時、ベクトルは\(\boldsymbol{10a}\)と表され、\(\boldsymbol{10a}\)の大きさ（\(\boldsymbol{|10a|}\)）は5×10=50となる。
ちなみに、ベクトル\(\boldsymbol{a}\)に対して、その大きさ\(\boldsymbol{|a|}\)の逆数\(\frac{1}{\boldsymbol{|a|}}\)をスカラー倍した
の大きさは、当然ながら「1」になります。よって、このベクトルは「単位ベクトル」となります。
ベクトルの計算上の性質
ベクトルの足し算（引き算）やスカラー倍の計算には次のような性質があります。
足し算の性質
つまり、足す順序は答えに影響しません！
つまり、3つの足し算が並んだ時、前の2つから足そうが、後ろ2つから足そうが結果が変わらないということです。
一般的に、足し算は「2つを足す」ことしか定義されていないので、3つの足し算は、2つの足し算の繰り返しになります。そのような時に、足し合わせる順番が結果に影響しないというのは、計算する上で考えなければいけないことが減る点でありがたいです。
要は、あるベクトルと、その逆ベクトル（逆向きのベクトル）を足し合わせると、零ベクトルになるということです。実際に足して見ると分かりますが、結局戻ってくるので、始点と終点が一緒になって零ベクトルとなります。
スカラー倍の性質
つまり、スカラーを最初に全部掛けた上でベクトルにどかっとスカラー倍しようが、ベクトルに対して次々にスカラー倍しようが、結果は変わらないということです。
「ベクトルの」分配法則ですね。「和」をスカラー倍しても、スカラー倍した2つのベクトルを足しても、結果は変わらないということです。スカラー同士の計算でも、ベクトル同士の計算でも結果が同じってことを言いたいわけです。
今度は、「スカラーの」分配法則です。「ベクトルの和」をスカラー倍しても、スカラー倍したベクトル同士を足し合わせても結果が同じということです。
1をスカラー倍してもベクトルは変わりません。だって、ベクトルの大きさに1を掛けても、大きさはそのままですからね笑
終わりに
今回は、高校で習ってきた「向きと大きさ」の観点で定義されたベクトルについて、その基本と計算の性質を扱いました。今まで線形代数で学んできた、数字の並びとしての「ベクトル」とはだいぶ毛色が異なりますよね笑
次回の記事は、ベクトルの内積を復習すると共に、「外積」という概念についても扱います！
