【線形空間編】シュミットの直交化法を画像で直感的に解説

こんにちは、おぐえもん(@oguemon_com)です。

前回の記事では、正規直交基底と直交行列を扱いました。

正規直交基底の作り方として「シュミットの直交化法（グラム・シュミットの正規直交化法）」というものを取り上げました。でも、これって数式だけを見ても意味不明です。そこで、今回は、画像を用いた説明を通じて、どんなことをしているのかを直感的に分かってもらいたいと思います！

シュミットの直交化法のおさらい

まずはシュミットの直交化法とは何かについて復習しましょう。

できること

シュミットの直交化法では、ある線形空間の基底をなす 1 次独立な$n$本のベクトルを用意して、色々計算を頑張ることで、その線形空間の正規直交基底を作ることができます！

たとえ、ベクトルの長さがバラバラで、ベクトル同士のなす角が直角でなかったとしても、シュミットの直交化法の力で、全部の長さが 1 で、互いに直交する 1 次独立なベクトルを生み出せるのです。

手法の流れ（難しい数式版）

シュミットの直交化法を数式で説明すると次の通り。初学者の方は遠慮なく読み飛ばしてください笑

簡単に書くとこんな感じです。正規化の Step はまだ簡単ですが、直交化の Step は数式が複雑でいまいちよく分からないと思います。次は画像を使って直交化の Step を直感的に捉えてみましょう。

直交化の処理を画像で表す

シュミットの直交化法そのものは、あらゆる次元の空間に対応するのですが、ここでは 3 次元空間を例にして直交化の流れを図解していきます。

一を聞いて十を悟る賢い人のためにオチを申しますと、「毎度$\boldsymbol{a_i}$から下ろした垂線そのものを$\boldsymbol{x_i}$としている」ってことです。$\boldsymbol{x_2}$は、$\boldsymbol{a_2}$の先端から"線"に下ろした垂線であり、$\boldsymbol{x_3}$は、$\boldsymbol{a_3}$の先端から"平面"に下ろした垂線なんですよ。どういうことか今から図解します。

前提

ここでは 1 次独立な 3 本の空間ベクトルを用意して、シュミットの直交化法を適用します。用意したベクトルはこんな感じ。

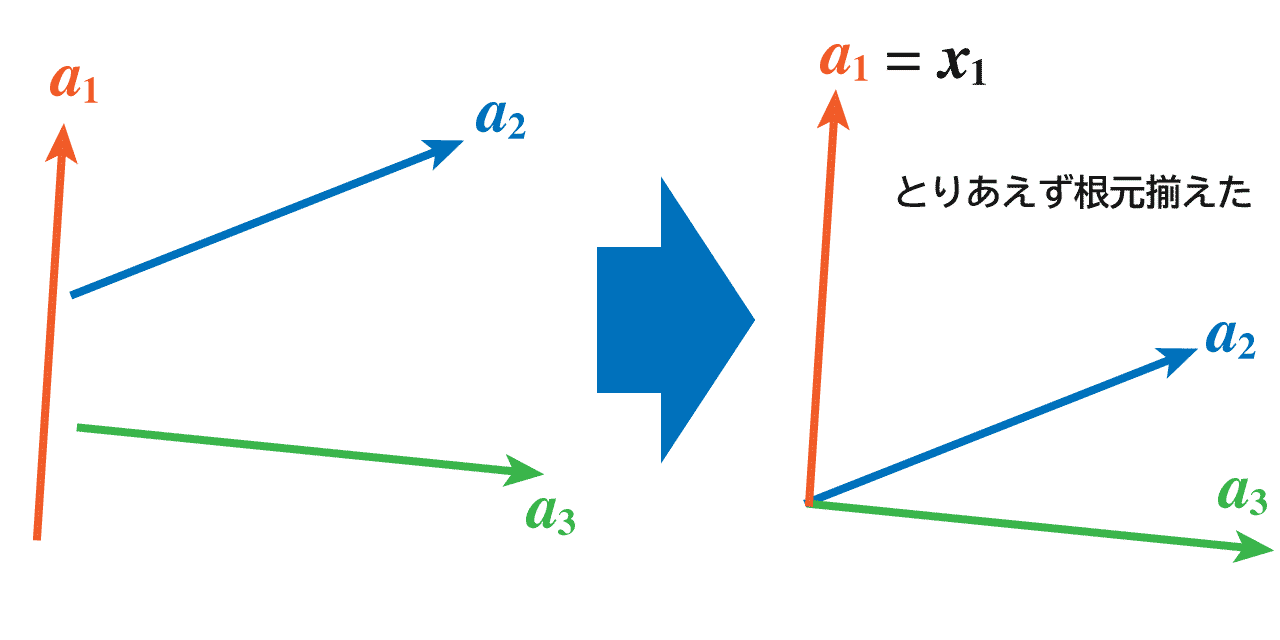
画像の左側のように、ベクトルはそれぞれバラバラの方向を向いています。ただし、1 次独立なので、3 本は同じ平面にはありません。ベクトルはどこへ動かしても同じなので、比較しやすいようにベクトルの根元を揃えました。

ここから新しく$\boldsymbol{x_1}$〜$\boldsymbol{x_3}$を作っていきます。

1本目のベクトル作り

$\boldsymbol{x_1}$は$\boldsymbol{a_1}$とします。それだけです。

$$\boldsymbol{x_1} \leftarrow \boldsymbol{a_1}$$

2本目のベクトル作り

さて、ここからが本番。$\boldsymbol{x_2}$の作り方です。次の式から求められるのでしたよね。

$$\boldsymbol{x_2} \leftarrow \boldsymbol{a_2} - \frac{(\boldsymbol{a_2},\boldsymbol{x_1})}{(\boldsymbol{x_1},\boldsymbol{x_1})}\boldsymbol{x_1}$$

え？意味不明？そう慌てなさんな。ここで、実は$\boldsymbol{x_2}$を生成するために、$\boldsymbol{a_2}$と$\boldsymbol{x_1}$の 2 本のベクトルしか使っていないことに着目！そこで、さっきの画像から、「$\boldsymbol{a_2}$と$\boldsymbol{x_1}$」を抽出して考えます。

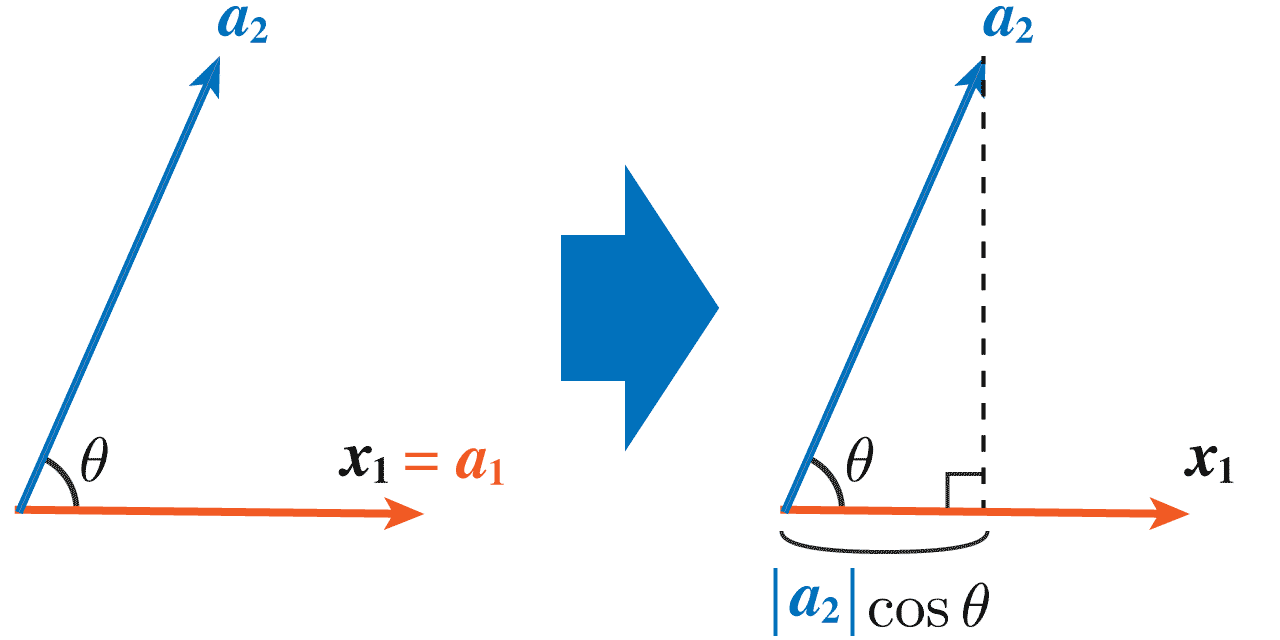
2 本のベクトルは、画像の左のような感じで配置しています。ここで、2 ベクトルのなす角は$\theta$としました。このとき、画像の右のように、$\boldsymbol{a_2}$の先端から$\boldsymbol{x_1}$（$\boldsymbol{a_1}$と同じ）へ垂線を下ろすと、根元から垂線の足までの距離は$|\boldsymbol{a_2}|\cos\theta$になりますよね。まずはこのことをしっかり押さえておきましょう！

さて、ここで、上の式の最後の項（$\frac{(\boldsymbol{a_2},\boldsymbol{x_1})}{(\boldsymbol{x_1},\boldsymbol{x_1})}\boldsymbol{x_1}$）が何を表すかについて考えます。複雑な形こそしていますが、展開＆約分することでその姿が見えてきます。

$$\begin{aligned} \frac{(\boldsymbol{a_2},\boldsymbol{x_1})}{(\boldsymbol{x_1},\boldsymbol{x_1})}\boldsymbol{x_1} &=\frac{|\boldsymbol{a_2}||\boldsymbol{x_1}|\cos \theta}{|\boldsymbol{x_1}|^2}\boldsymbol{x_1}\\ &=|\boldsymbol{a_2}|\cos \theta \frac{1}{|\boldsymbol{x_1}|}\boldsymbol{x_1} \end{aligned}$$

最後の式を「$|\boldsymbol{a_2}|\cos\theta$」と、「$\frac{1}{|\boldsymbol{x_1}|}\boldsymbol{x_1}$」に分けて考えましょう。まず、前者は、先ほどの根元から垂線の足までの距離ですね。そして、後者は、「$\boldsymbol{x_1}$と同じ向きで長さが 1 のベクトル」です。つまり、後者のベクトルに、前者のスカラーを掛け合わせることで、「根元から垂線の足までの距離を長さにもつ、$\boldsymbol{x_1}$と同じ向きのベクトル」が爆誕するわけです！

つまり、このベクトルは次の画像の左側で示したものに相当します。

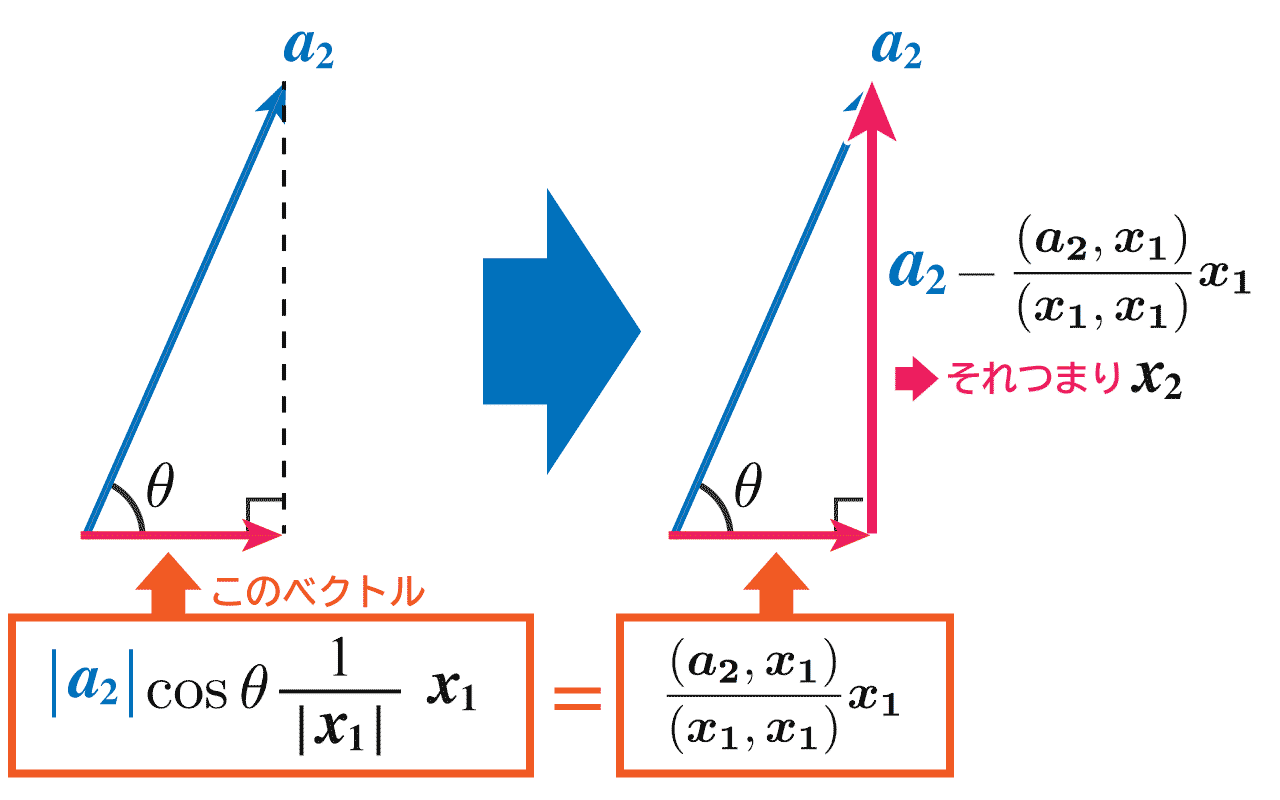
$\boldsymbol{x_2}$は、$\boldsymbol{a_2}$からこのベクトルを引くことで生み出せます。もうお判りだと思いますが、画像の右側で示したように、$\boldsymbol{x_2}$は、$\boldsymbol{a_2}$の先端から$\boldsymbol{x_1}$上にたらした垂線そのものになるわけです。そりゃ、$\boldsymbol{x_2}$と$\boldsymbol{x_1}$は直交しますわな。

3本目のベクトル作り

次に、3 本目のベクトル$\boldsymbol{x_3}$を作りましょう。これは次の式で求められました。

$$\boldsymbol{x_3} \leftarrow \boldsymbol{a_3} - \Bigl(\frac{(\boldsymbol{a_3},\boldsymbol{x_1})}{(\boldsymbol{x_1},\boldsymbol{x_1})}\boldsymbol{x_1} + \frac{(\boldsymbol{a_3},\boldsymbol{x_2})}{(\boldsymbol{x_2},\boldsymbol{x_2})}\boldsymbol{x_2}\Bigr)$$

ますます複雑！しかし、原理は$\boldsymbol{x_2}$を求めた時とそう変わりません。

ここでは、既に求めた互いに直交なベクトル$\boldsymbol{x_1}$＆$\boldsymbol{x_2}$と、新しいベクトル$\boldsymbol{a_3}$が登場人物となります。そこで、この 3 ベクトルのみを抜き出して考えます。次の画像の左側みたいな感じですね。賢いみなさんは「どうせ垂線使うんだろオラ！」と思っていることでしょうし、$\boldsymbol{a_3}$の先端からそれぞれのベクトルに垂線を下ろしておきました（画像の右側）。

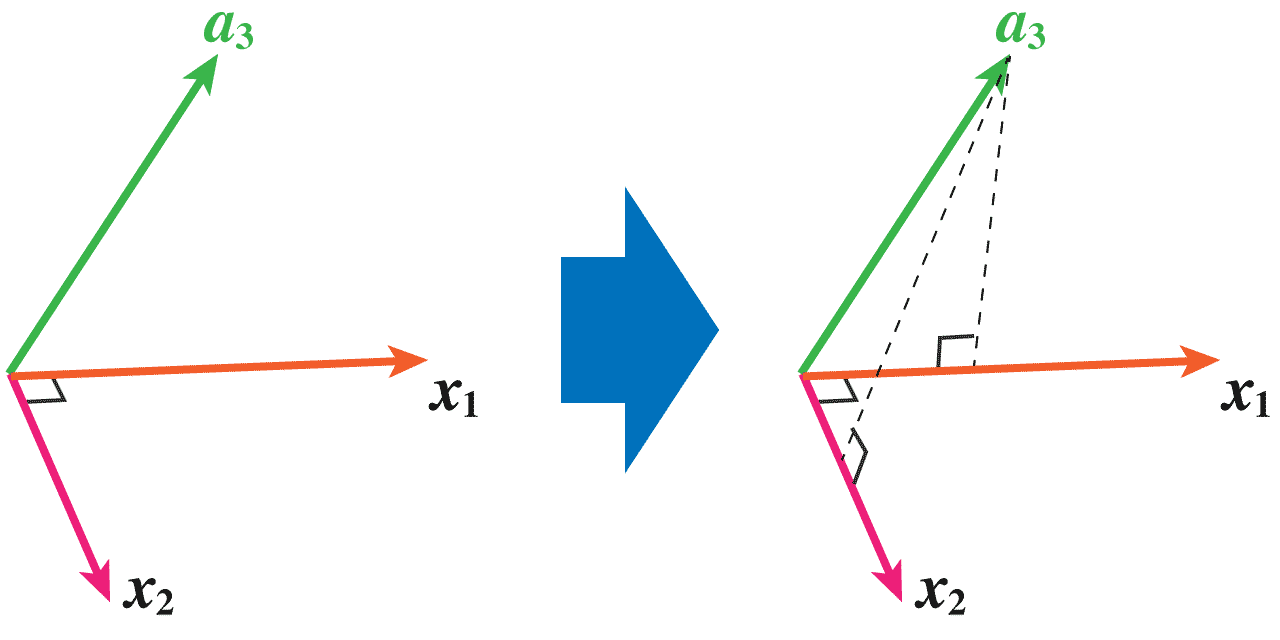
賢いみなさんの予想はズバリ的中です！上の式を構成する後ろの 2 項（$\frac{(\boldsymbol{a_3},\boldsymbol{x_1})}{(\boldsymbol{x_1},\boldsymbol{x_1})}\boldsymbol{x_1}$と$\frac{(\boldsymbol{a_3},\boldsymbol{x_2})}{(\boldsymbol{x_2},\boldsymbol{x_2})}\boldsymbol{x_2}$）は、$\boldsymbol{x_2}$を求めたときみたく、それぞれ、次の画像の左側に示したベクトルを表すのです。そして、画像で平面的に表現しているのですごく分かりにくいのですが、この 3 つのベクトルって実は画像の右側のように直方体を形作っています。

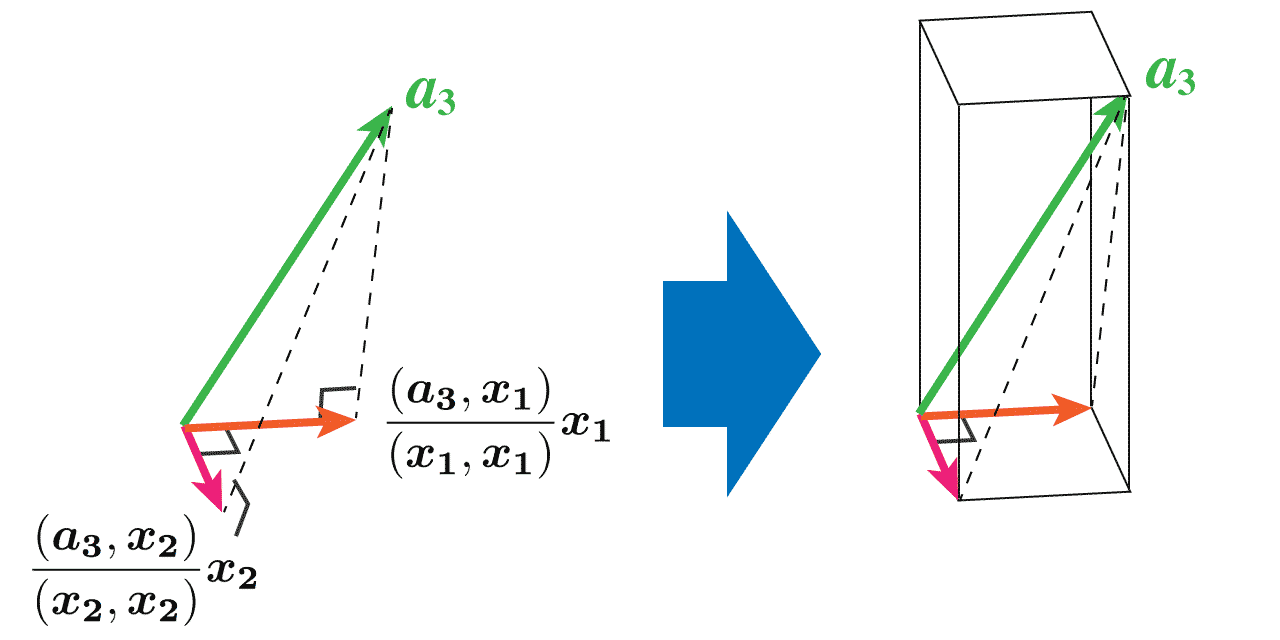
ここまできたら、$\boldsymbol{x_3}$まであと少し。次の画像の左側にある水色のベクトルは、先ほどの 2 ベクトルを足し合わせたものです。そして、$\boldsymbol{a_3}$からこのベクトルを引くと、画像の右側における赤いベクトルとなります。

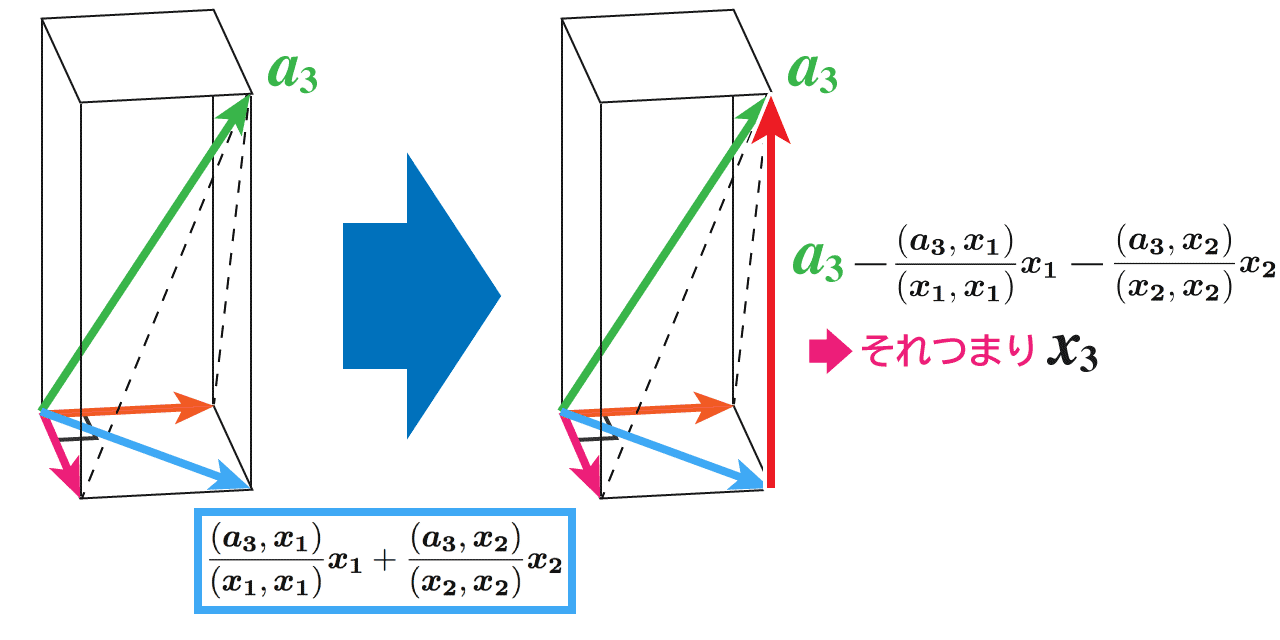
お判りいただけると思いますが、これって、$\boldsymbol{x_1}$と$\boldsymbol{x_2}$が作る平面に対して$\boldsymbol{a_3}$から下ろした垂線そのものなんですね。そりゃ、$\boldsymbol{x_3}$と$\boldsymbol{x_2}$、$\boldsymbol{x_3}$と$\boldsymbol{x_1}$はともに直交しますわな。

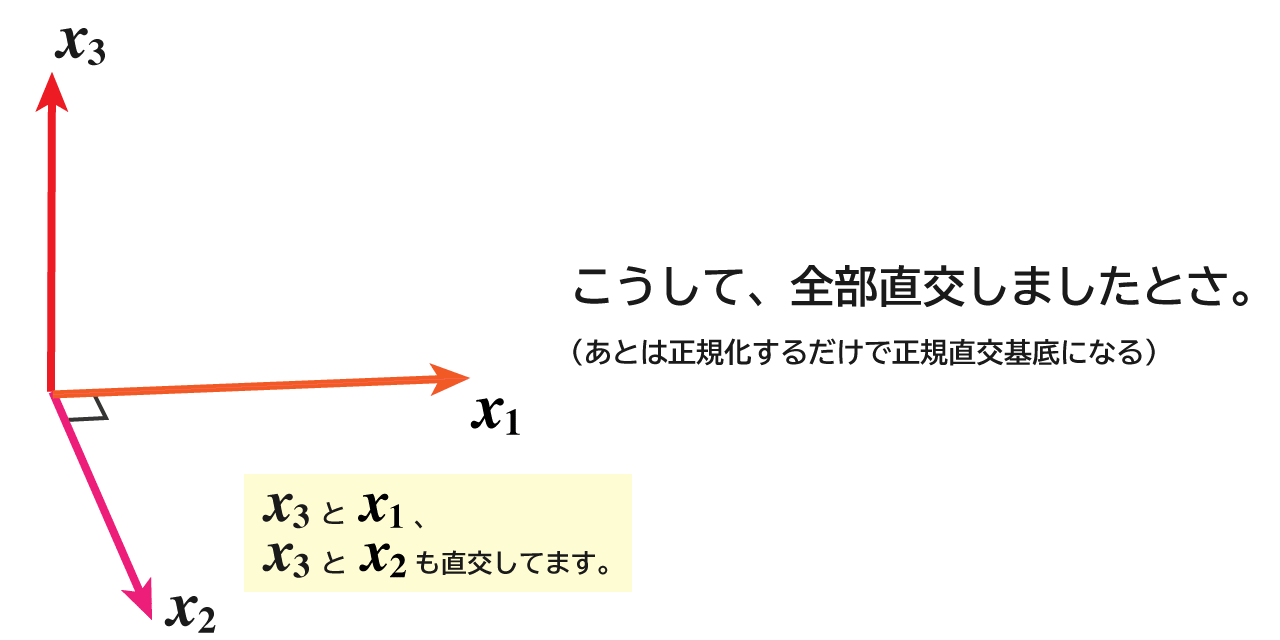
以上の図解を通じて、この章の冒頭で述べたオチ「$\boldsymbol{a_i}$から下ろした垂線そのものを$\boldsymbol{x_i}$としている」の意味が直感的にお分かりいただけたかと思います。

おわりに

今回は、複雑な数式が並ぶシュミットの直交化法について、3 次元の空間ベクトルを例にしてその方法を図解しました。

これで線形空間編は終わりです！